Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn: Chọn đáp án B

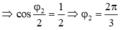
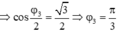
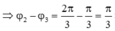
=> Chọn B
Chú ý: Khi cho biết A, j1, j2 tìm điều kiện để A1 max hoặc A2 max ta viết lại hệ thức:
![]()
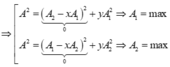

Đáp án A
Do x 1 v à x 2 vuông pha nên x 1 A 1 2 + x 2 A 2 2 = 1
Tương tự x 2 v à x 3 vuông pha nên: x 2 A 2 2 + x 3 A 3 2 = 1
Tại thời điểm t 2 : - 20 A 1 2 + 0 A 2 2 = 1 ⇒ A 1 = 20 c m
Tại thời điểm t 1
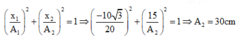
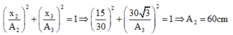
Từ giản đồ Frenel (hình vẽ) ta có: A = A 2 2 + ( A 3 - A 1 2 ) = 50 c m

Ta có $x_1=x_{12}-x_2=x_{12}-(x_{23}-(x_{13}-x_1)$
$\Rightarrow$ $2x_1=x_{12}-x_{23}+x_{13}$. Bấm máy tính ta được
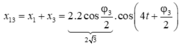
${x_1}={3\sqrt{6}}\cos\left({\pi t + \dfrac{\pi}{12}} \right)$
${x_3}={3\sqrt{2}}\cos\left({\pi t + \dfrac{7\pi}{12}} \right)$
Suy ra hai dao động vuông pha, như vậy khi x1 đạt giá trị cực đại thì x3 bằng 0.
![]()
cách bấm máy để ra phương trình dao động làm như thế nào vậy ạ

Hướng dẫn: Chọn đáp án A
![]()
![]()
=>Chọn A
Dùng máy tính Casio fx 570 – ES, bấm như sau:
Shift MODE 4 (Để chọn đơn vị góc là radian)
MODE 2 (Để chọn chế độ tính toán với số phức)
![]()
(Màn hình máy tính sẽ hiển thị 6 3 - 10 ∠ π 2 - 12 ∠ π 6 )
Shift 2 3 =
Màn hình sẽ hiện kết quả: 16 ∠ - 1 2 π
Nghĩa là biên độ A 3 = 16 c m và pha ban đầu φ 3 = - 1 2 π nên ta sẽ chọn A.
Chú ý: Để tính biên độ thành phần ta dựa vào hệ thức:
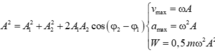


+ Do x1 và x2 vuông pha nên: x 1 A 1 2 + x 2 A 2 2 = 1
+ Tương tự x2 và x3 vuông pha: x 2 A 2 2 + x 3 A 3 2 = 1
+ Tại thời điểm t 2 : − 20 A 1 2 + 0 A 2 2 = 1 ⇒ A 1 = 20 c m
+ Tại thời điểm t 1 : x 1 A 1 2 + x 2 A 2 2 = 1 ⇒ − 10 3 20 2 + 15 A 2 2 = 1 ⇒ A 2 = 30 c m
x 2 A 2 2 + x 3 A 3 2 = 1 ⇒ 15 30 2 + 30 3 A 1 2 = 1 ⇒ A 3 = 60 c m
+ Từ giản đồ: A = A 2 2 + A 3 − A 1 2 = 50 c m
Chọn đáp án A

Chọn đáp án B
Nhận thấy x 1 và x 3 ngược pha nhau và cùng vuông pha với x 2 nen tại thời điểm t 2 thì x 2 = 0 nên
x 1 = − 20 c m = − A 1 ; x 3 = 60 c m = A 3
Mặt khác x 1 vuông pha x 2 nên tại thời điểm t 1 ta có:
− 10. 3 2 20 2 + 15 2 A 2 2 = 1 ⇒ A 2 = 30 .
Biên độ dao động tổng hợp:
A = A 1 − A 3 2 + A 2 2 = 40 2 + 30 2 = 50 c m

\(x=x_1+x_2\Rightarrow x_2=x-x_1=2-5=-3cm\)
Ta có: \(x_1=10\cos(5\pi t)=5\Rightarrow 5\pi t=\pi/3\)
Suy ra \(x_2=A_2\cos(\dfrac{\pi}{3}+\dfrac{\pi}{3})=-0,5A_2=-3\)
\(\Rightarrow A_2 = 6cm\)
Vậy biên độ tổng hợp: \(A^2=10^2+6^2+2.10.6\cos(\pi/3)=196\)
\(\Rightarrow A = 13cm\)
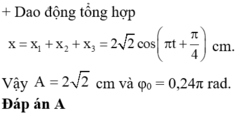

+ Phương pháp giản đồ vecto
+ Từ hình vẽ, ta thấy rằng A2 ≤ OH.
Áp dụng hệ thức lượng trong tam giác, ta thu được
Đáp án A