PA
1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Các câu hỏi dưới đây có thể giống với câu hỏi trên
TH
1
AH
Akai Haruma
Giáo viên
15 tháng 3 2018
Lời giải:
\(z=x+yi\Rightarrow |z|=\sqrt{x^2+y^2}=1(1)\)
\(y=\sqrt{3}x; y>0\Rightarrow \left\{\begin{matrix} x>0\\ y^2=3x^2(2)\end{matrix}\right.\)
Từ \((1); (2)\Rightarrow \sqrt{x^2+3x^2}=1\Leftrightarrow 2x=1\Leftrightarrow x=\frac{1}{2}\)
\(\Rightarrow y=\frac{\sqrt{3}}{2}\)
Số phức \(z=\frac{1}{2}+\frac{\sqrt{3}i}{2}\)
\(\Rightarrow z-\frac{1}{z}+1=1+\sqrt{3}i\)
\(\Rightarrow |z-\frac{1}{z}+1|=\sqrt{1^2+3}=2\) (đây chính là mo đun của số phức đã cho )
NV
Nguyễn Việt Lâm
Giáo viên
3 tháng 7 2020
Phương trình tham số d1: \(\left\{{}\begin{matrix}x=1+2t\\y=3+3t\\z=2t\end{matrix}\right.\)
Phương trình tham số d2: \(\left\{{}\begin{matrix}x=5+6t'\\y=4t'\\z=5-5t'\end{matrix}\right.\)
Gọi (Q) là mặt phẳng song song (P) và cách (P) 1 khoảng bằng 2 \(\Rightarrow\) pt có dạng \(x-2y-2z-d=0\) (\(d\ne1\))
Gọi \(A\left(d;0;0\right)\) là 1 điểm thuộc (Q)
\(d\left(A;\left(P\right)\right)=2\Leftrightarrow\frac{\left|d+1\right|}{\sqrt{1+4+4}}=2\Leftrightarrow\left|d+1\right|=6\Rightarrow\left[{}\begin{matrix}d=5\\d=-7\end{matrix}\right.\)
Có 2 mp (Q) thỏa mãn: \(\left[{}\begin{matrix}x-2y-2z-5=0\\x-2y-2z+7=0\end{matrix}\right.\)
M là giao điểm (Q) và d1 nên tọa độ M là ...
N là giao điểm (Q) và d2 nên tọa độ N là ...
TX
1
NV
Nguyễn Việt Lâm
Giáo viên
6 tháng 4 2022
(S) có tâm \(I\left(m-3;2m;-1\right)\)
Để I thuộc (P) \(\Rightarrow m-3+2m-2.\left(-1\right)-3=0\)
\(\Rightarrow3m-4=0\Rightarrow m=\dfrac{4}{3}\)
CM
2 tháng 11 2017
Chọn A.
Các mặt phẳng đôi một vuông góc và có một điểm chung.
CM
8 tháng 2 2017
Chọn C
Phương trình tham số của đường thẳng Δ: 
Gọi tâm I ∈ Δ => I (3+2t;1-t;1-2t)
Vì mặt cầu (S) đồng thời tiếp xúc với hai mặt phẳng (α1) và (α2) nên ta có
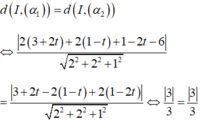
Do đó có vô số mặt cầu thỏa yêu cầu đề bài.
HN
10 tháng 5 2018
M∈ (S) : (x0 - 2)2 + (y0-1)2 +(z0-1)2 =9.
A=x0+2y0+2z0=(x0-2)+2(y0-1)+2(z0-1)+6
Dùng BĐT bunhiacopski
[(x0-2)+2(y0-1)+2(z0-1)]2 ≤ (1+4+4).[(x0 - 2)2 + (y0-1)2 +(z0-1)2 ]
≤ 81
-9 ≤ (x0-2)+2(y0-1)+2(z0-1) ≤ 9.
-3 ≤ A ≤ 12. vậy GTNN của A = -3.
Dấu bằng xảy ra khi :
x0+2y0+2z0 = -3
và \(\dfrac{x0-2}{1}=\dfrac{y0-1}{1}=\dfrac{z0-1}{1}\)
Giải hệ được x0=1, y0=z0=-1. Suy ra: x0+y0+z0 = -1
AH
Akai Haruma
Giáo viên
8 tháng 1 2017
Gọi vecto chỉ phương của tiếp tuyến là \(\overrightarrow{u}_{(a,b,c)}\). Ta có :
\(\overrightarrow {AC}=(-1,-1,0);\overrightarrow {n}_{P}=(2,1,1)\)
Theo điều kiện đề bài \(\overrightarrow{u}\perp \overrightarrow{AC},\overrightarrow{u}\perp \overrightarrow{n}_{P}\Rightarrow \overrightarrow{u}=[\overrightarrow{AC},\overrightarrow{n}_{P}]=(-1,1,1)\)
Do đó phương tiếp tuyến có dạng \(\frac{x-2}{-1}=y-2=z\), tức đáp án $B$ là đáp án đúng
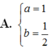
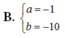
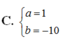
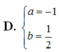
Lời giải:
$x\in \mathbb{Z}^+, y\in\mathbb{Z}^-$ thì $xy\in\mathbb{Z}^-$
Còn $x+y$ không xác định được là nguyên âm hay nguyên dương vì nó có thể xảy ra cả 2 TH:
x=5, y=-3 thì x+y nguyên dương
x=1, y=-3 thì x+y nguyên âm.