Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử p ≠ 0 ta có:
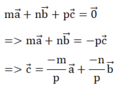
Do đó, ba vecto a → , b → , c → đồng phẳng theo định lí 1

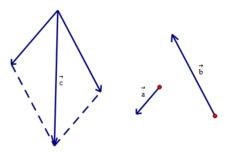
a → , b → , c → đồng phẳng vì a → và b → không cùng phương và có cặp số (2; -1) sao cho c → = 2 a → - b →

Nếu hai trong ba vecto đó cùng hướng thì ba vecto đồng phẳng; nếu hai trong ba vecto đó không cùng hướng thì chưa thể kết luận được ba vecto đó đồng phẳng.
Đáp án C

\(2\overrightarrow{y}-\overrightarrow{z}=2\overrightarrow{a}-2\overrightarrow{b}-2\overrightarrow{c}+3\overrightarrow{b}+2\overrightarrow{c}=2\overrightarrow{a}+\overrightarrow{b}=\overrightarrow{x}\)
\(\Rightarrow\) Ba vecto \(\overrightarrow{x},\overrightarrow{y},\overrightarrow{z}\) đồng phẳng
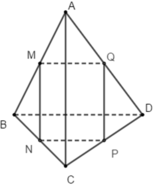

Phương án A và C sai vì có thể xảy ra trường hợp như hình vẽ sau
Giả sử phương án B cũng sai, tức là ba vecto n → , a → v à b → đồng phẳng. Khi đó vì n→ ⊥ a→ và n→ ⊥ b→ nên giá của a → v à b → song song. Điều này mẫu thuẫn với giả thiết hai vecto a → v à b → không cùng phương. Vì vậy phương án B đúng.
Đáp án B