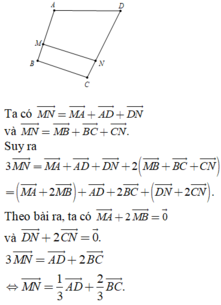Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi E, F lần lượt là trung điểm AC và BD
Đặt \(\frac{AM}{AD}=\frac{CN}{CB}=k\Rightarrow\left\{{}\begin{matrix}\overrightarrow{AM}=k.\overrightarrow{AD}\\\overrightarrow{CN}=k.\overrightarrow{CB}\end{matrix}\right.\) với k là hằng số
\(\overrightarrow{EI}=\overrightarrow{EC}+\overrightarrow{CN}+\overrightarrow{NF}=\frac{1}{2}\overrightarrow{AC}+\overrightarrow{CN}+\frac{1}{2}\overrightarrow{NM}\)
\(=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{DC}\right)+\overrightarrow{CN}+\frac{1}{2}\left(\overrightarrow{NC}+\overrightarrow{CD}+\overrightarrow{DM}\right)\)
\(=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC}+\overrightarrow{CN}+\frac{1}{2}\overrightarrow{NC}+\frac{1}{2}\overrightarrow{CD}+\frac{1}{2}\overrightarrow{DM}\)
\(=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{CN}+\frac{1}{2}\overrightarrow{DM}=\frac{1}{2}\overrightarrow{AM}+\frac{1}{2}\overrightarrow{CN}=\frac{k}{2}\left(\overrightarrow{AD}+\overrightarrow{CB}\right)\)
\(\overrightarrow{EF}=\overrightarrow{EC}+\overrightarrow{CB}+\overrightarrow{BF}=\frac{1}{2}\overrightarrow{AC}+\overrightarrow{CB}+\frac{1}{2}\overrightarrow{BD}\)
\(=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{DC}+\overrightarrow{CB}+\frac{1}{2}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CD}\)
\(=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{CB}=\frac{1}{2}\left(\overrightarrow{AD}+\overrightarrow{CB}\right)\)
\(\Rightarrow\overrightarrow{EF}=k.\overrightarrow{EI}\Rightarrow E;F;I\) thẳng hàng hay I luôn thuộc đường thẳng EF cố định

\(\overrightarrow{AB}+\overrightarrow{CD}=\overrightarrow{AB}+\overrightarrow{CB}+\overrightarrow{BD}=\overrightarrow{AB}+\overrightarrow{BD}+\overrightarrow{CB}=\overrightarrow{AD}+\overrightarrow{CB}\)
\(\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}+\overrightarrow{OD}=\left(\overrightarrow{OE}+\overrightarrow{EA}\right)+\left(\overrightarrow{OF}+\overrightarrow{FB}\right)+\left(\overrightarrow{OE}+\overrightarrow{EC}\right)+\left(\overrightarrow{OF}+\overrightarrow{FD}\right)\)
\(=2\left(\overrightarrow{OE}+\overrightarrow{EF}\right)+\left(\overrightarrow{EA}+\overrightarrow{EC}\right)+\left(\overrightarrow{FB}+\overrightarrow{FD}\right)\)
\(=2.\overrightarrow{0}+\overrightarrow{0}+\overrightarrow{0}=\overrightarrow{0}\)