Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Gọi giao của $BO$ và $AC$ là $H$
Vì $BA=BC; OA=OC$ nên $BO$ là trung trực của $AC$
$\Rightarrow BO$ vuông góc với $AC$ tại trung điểm $H$ của $AC$.
Do đó $HO$ là đường trung bình ứng với cạnh $CD$ của tam giác $ACD$
$\Rightarrow HO=2$
$BH=BO-HO=R-2$
Theo định lý Pitago:
$BC^2-BH^2=CH^2=CO^2-HO^2$
$\Leftrightarrow (4\sqrt{3})^2-(R-2)^2=R^2-2^2$
$\Leftrightarrow 48-(R-2)^2=R^2-4$
$\Rightarrow R=6$ (cm)

1. Ta có AD // OM // BC ; OA = OB
=> OM là đường trung bình của hình thang ABCD => M là trung điểm CD => MC = MD
2. Vì OM là đường trung bình của hình thang ABCD nên : \(OM=\frac{AD+BC}{2}\Rightarrow AD+BC=2OM\)không đổi.
3. Dễ thấy M là tâm của đường tròn đường kính CD vì MC = MD
Lại có AD vuông góc với MD => đpcm
4. Ta có : \(S_{ABCD}=\frac{1}{2}.\left(AD+BC\right).CD=OM.CD\)
Vì OM không đổi nên S.ABCD lớn nhất <=> CD lớn nhất <=> CD = AB
Vậy max (S.ABCD) = OM . AB = R.(2R) = 2R2 với R = AB/2

Nhận xét: tam giác OAD = OBC (Vì OA = OB ; OD = OC; AD = BC = 2\(\sqrt{5}\))
=> S DAO = SCBO mà 2 đáy OA = OB
=> đường cao DK = CH
Dễ dang => CD // AB do đó, CH = DK = OE
Gọi bán kính đtr = R
Xét tam giác vuông OED có: OE2 = R2 - 32 = R2 - 9
=> DK2 = R2 - 9
+) Mặt khác, dễ có: CD = HK và OH = OK
=> OK = HK/ 2 = 6/2 = 3cm
=> AK = R - 3 (cm)
+) Xét tam giác vuông AKD có: DK2 + AK2 = AD2
=> R2 - 9 + (R - 3)2 = (2\(\sqrt{5}\))2
=> 2.R2 - 6R = 20
=> R2 - 3R - 10 = 0
<=> R2 - 5R + 2R - 10 = 0
<=> (R - 5)(R + 2) = 0 => R = 5 hoặc R = -2 mà R > 0
Vậy R = 5cm
)

AC=AD
OC=OD
=>AO là trung trực của CD
=>OA vuông góc CD tại I
góc AMB=1/2*180=90 độ
góc KMB+góc KIB=180 độ
=>KMBI nội tiếp

Ta có : A là giao điểm của 2 đường tiếp tuyến tại E và G của O =>AG=AE
Chứng minh tương tự,ta được BE=BH
=>AG+BH=AB
Tương tự,ta có DG+HC=CD
=>AB+CD=AD+BC=10cm
nửa đường tròn tâm G: 2AG.π/2=AG.π=1/2.AD.π
nửa đường tròn tâm H:1/2.BC.π
=> S=1/2(AD+BC)π=5π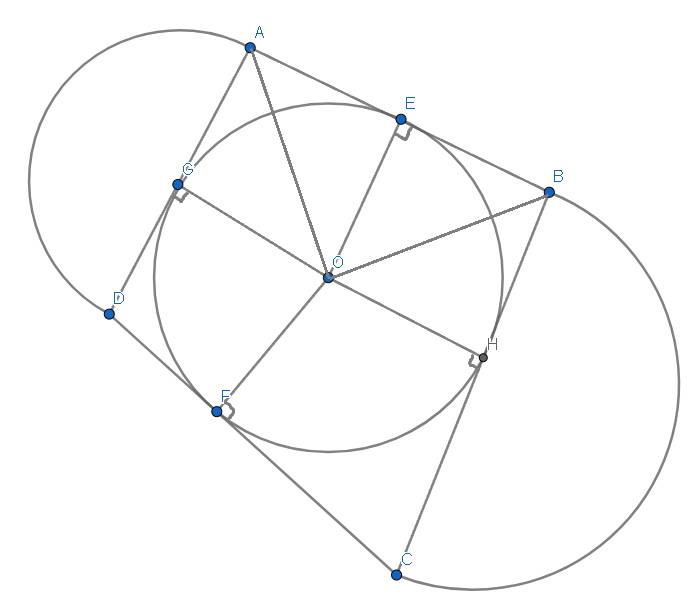

a,Xét tứ giác ACHI có: góc ACB = 90o (góc nội tiếp chắn nửa đường tròn)
góc HIA = 90o (gt)
=> tổng hai góc này =180o mà đỉnh C và I lại nằm ở vị trí đối nhau => tứ giác ACHI là tứ giác nội tiếp đường tròn đường kính AH (đpcm)