Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn (khuya quá rồi).
Trong mp (ADN), lấy Q thuộc AD sao cho \(NP||GQ\)
\(\Rightarrow\left(\overrightarrow{MG};\overrightarrow{NP}\right)=\left(\overrightarrow{MG};\overrightarrow{GQ}\right)=180^0-\widehat{MGQ}\)
Áp dụng định lý hàm cos là tính được (\(GP=\dfrac{2}{3}NP\) ; tính MQ dựa vào hàm cos tam giác AMQ)

\(\overrightarrow{AB}.\overrightarrow{BD}=-\overrightarrow{BA}.\overrightarrow{BD}=-a.a.cos60^0=-\dfrac{a^2}{2}\)

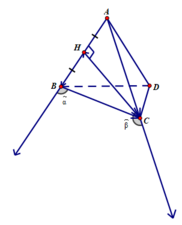
Tứ diện ABCD đều có các mặt là tam giác đều
a) Góc giữa A B → v à B C → là góc α ^ và
α ^ = 180 o - 60 o = 120 o
b) Góc giữa C H → v à A C → là β ^
H là trung điểm cạnh AB của tam giác đều ABC nên CH vừa là trung tuyến vừa là đường cao nên CH ⊥ AB
Xét tam giác vuông ACH tại H có
A C H ^ + H A C ^ = 90 o ⇒ A C H ^ = 90 o - 60 o = 30 o
Nên β ^ = 180 o - 30 o = 150 o

\(BD=a\sqrt{2}\)
\(\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=\widehat{SBD}=\dfrac{SB^2+BD^2-SD^2}{2SB.BD}=\dfrac{a^2+2a^2-a^2}{2a.a\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
\(\Rightarrow\widehat{\left(\overrightarrow{BD};\overrightarrow{BS}\right)}=45^0\)
thầy ơi bưa trước thầy em có giảng cái cách mà SB=SD thì suy ra SBD là nửa hình vuông nên góc SBD 45 độ v đúng ko thầy?

\(\overrightarrow{AC}+\overrightarrow{BD}=\overrightarrow{AM}+\overrightarrow{MN}+\overrightarrow{NC}+\overrightarrow{BM}+\overrightarrow{MN}+\overrightarrow{ND}\)
\(=2\overrightarrow{MN}+\left(\overrightarrow{AM}+\overrightarrow{BM}\right)+\left(\overrightarrow{NC}+\overrightarrow{ND}\right)\)
\(=2\overrightarrow{MN}\)
\(\Rightarrow k=\dfrac{1}{2}\)

Gọi MM là trung điểm của CD.
Ta có CD→.AM→=0→ và CD→.MB→=0→.
Do đó →CD.→AB=→CD.(→AM+→MB)=→CD.→AM+→CD.→MB=⃗0
Suy ra AB⊥CD nên số đo góc giữa hai đường thẳng AB và CD bằng 900.