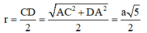Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
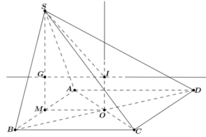
Gọi M là trung điểm của CD đường thẳng qua M song song với AC cắt AD tại trung điểm I của AD. Khi đó I là tâm mặt cầu ngoại tiếp khối tứ diện


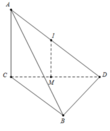
Ta có A D C ^ = A B C ^ = 60 ° , suy ra tam giác ADC là tam giác đều cạnh a. Gọi N là trung điểm cạnh DC, G là trọng tâm của tam giác ABC. Ta có A N = a 3 2 ; A G = a 3 3
Trong mặt phẳng (SAN), kẻ đường thẳng Gx//SA, suy ra Gx là trục của tam giác ADC.
Gọi M là trung điểm cạnh SA. Trong mặt phẳng (SAN) kẻ trung trực của SA cắt Gx tại I thì IS=IA=ID=IC nên I chính là tâm mặt cầu ngoại tiếp tứ diện S.ACD. Bán kính R của mặt cầu bằng độ dài đoạn IA.
Trong tam giác AIG vuông tại G, ta có:
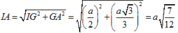

Đáp án là B

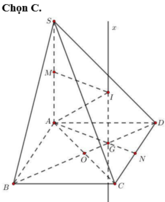
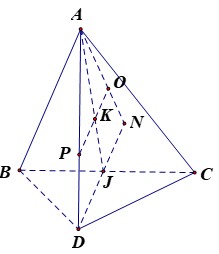
Gọi K là trọng tâm tam giác ABC, N đỗi xứng với D qua J, qua K kẻ KO song song với DN ta có O là tâm mặt cầu cần xác định.
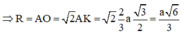

Đáp án A
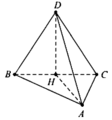
Gọi H là trung điểm của BC, O là tâm đường tròn ngoại tiếp tam giác ABC suy ra H là trung điểm của AO.
Ta có D H = 3. V A B C D S Δ A B C = a 3 4 .
Gọi J là tâm mặt cầu ngoại tiếp tứ diện ABCD.
Khi đó J O ⊥ A B C .
Do J A = R , O A = a nên J O = R 2 − a 2 .
Mặt khác H O ⊥ J O , H O ⊥ H D nên ta có
a 3 4 ± R 2 − a 2 2 + a 2 2 = R 2 ⇔ R = a 91 8 .





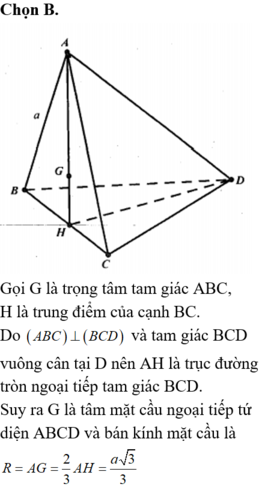
Đáp án D
Ta có: