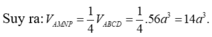Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


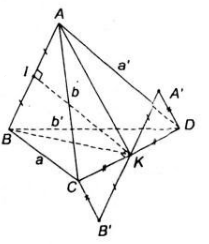
Hai tam giác ABC và BAD bằng nhau ( c.c.c) nên có các đường trung tuyến tương ứng bằng nhau: CM = DM
Ta có tam giác MCD cân tại M, do đó MN ⊥ CD vì N là trung điểm của CD. Tương tự ta chứng minh được NA = NB và suy ra MN ⊥ AB. Mặt phẳng (CDM) không vuông góc với mặt phẳng (ABN) vì (CDM) chứa MN vuông góc với chỉ một đường thẳng AB thuộc (ABN) mà thôi.

A B C D M N a c c a b d
Đặt \(AB=CD=c\), \(BC=DA=a\) , \(AC=b\) và \(BD=d\)
Do N là trung điểm cạnh BD nên theo công thức tính độ dài đường trung tuyến, ta có :
\(AN^2=\frac{c^2+a^2}{2}-\frac{d^2}{4}\) và \(CN^2=\frac{a^2+c^2}{2}-\frac{d^2}{4}\)
Suy ra : \(NA^2-NC^2=0=MA^2-MC^2\)
Từ đó theo kết quả bài toán suy ra \(MN\perp AC\)
Lập luận tương tự ta cũng được \(MN\perp BD\)

a: Gọi E là trung điểm của AB
ΔABC đều nên CE vuông góc AB
ΔABD đều nên DE vuông góc AB
=>AB vuông góc (CDE)
=>AB vuông góc CD
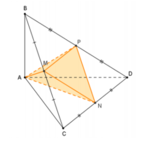
b: Xét ΔCAB có CN/CB=CM/CA
nên MN//AB và MN=1/2AB
Xét ΔDAB có DQ/DA=DP/DB
nên PQ//AB và PQ/AB=DQ/DA=1/2
=>MN//PQ và MN=PQ
=>MNPQ là hình bình hành
Xét ΔADC có AQ/AD=AM/AC
nên QM//DC
=>QM vuông góc AB
=>QM vuông góc QP
=>MNPQ là hình chữ nhật

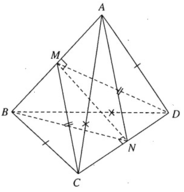
Gọi I, K lần lượt là trung điểm của cạnh AB và CD
Qua K kẻ đường thẳng d // AB, trên d lấy A', B' sao cho K là trung điểm của A'B' và
KA' = IA
* Xét tam giác CKB’ và DKA’ có:
KC= KD ( giả thiết)
KB’= KA’( cách dựng)
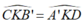 ( hai góc đối đỉnh )
( hai góc đối đỉnh )
=> ∆ CKB’ = ∆ DKA’ ( c.g.c)
=> B’C = A’D
*Xét tứ giác IBB’K có IB= KB’ và IB // KB’ ( cách dựng)
=> Tứ giác IBB’K là hình bình hành
=> BB’ // IK (1)
Chứng minh tương tự, ta có: AA’// IK (2)
Từ (1) và (2) suy ra: BB’// IK// AA’ (*)
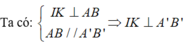
Lại có:IK ⊥ CK
=> IK ⊥ (CKB') (**)
Từ (*) và (**) suy ra BB' ⊥ (CKB') ; AA' ⊥ (CKB')
⇒ BB' ⊥ B'C; AA' ⊥ A'D
* Xét hai tam giác vuông BCB’ và ADA’ có:
BB’ = AA’ (= IK)
CB’ = A’D (chứng minh trên)
=> ∆ BCB’ = ∆ ADA’ ( cạnh huyền –cạnh góc vuông)
=> BC= AD.
* Chứng minh tương tự, AC = BD

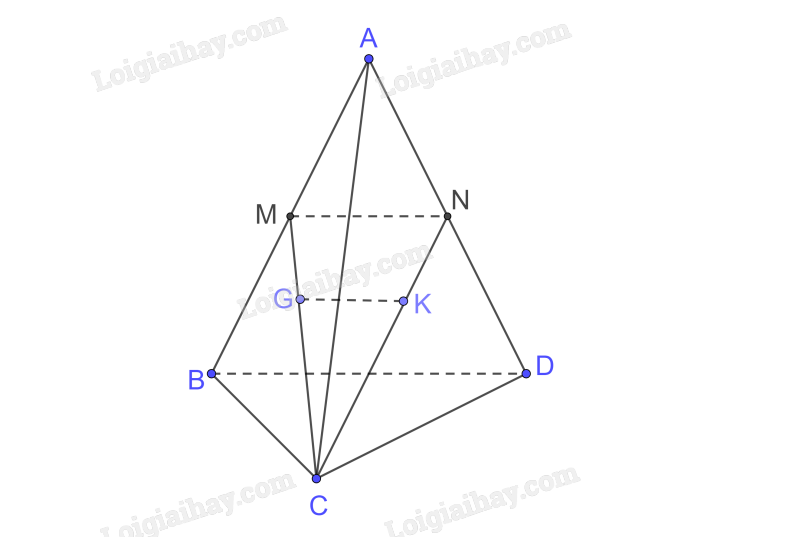
a) Xét tam giác ABD có
M, N tương ứng là trung điểm của AB, AD
\( \Rightarrow \) MN là đường trung bình của tam giác ABD
\( \Rightarrow \) MN // BD mà BD \( \bot \) BC (\(\widehat {CBD} = {90^0}\))
\( \Rightarrow \) MN \( \bot \) BC.
b) Vì G, K tương ứng là trọng tâm của các tam giác ABC, ACD nên \(\frac{{CG}}{{CM}} = \frac{{CK}}{{CN}} = \frac{2}{3}\)
\( \Rightarrow \) GK // MN (Định lý Talet) mà MN \( \bot \) BC
\( \Rightarrow \) GK \( \bot \) BC.