Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta tìm số cặp số (a;b) thoả mãn
![]()
![]()
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
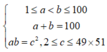
![]()
Do đó 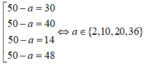
Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một số chính phương.

Chọn B
Số tập con của S là 2 6 = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là: 64 2
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử ![]()
Khi đó: A có C 6 x cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có C x 2 cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có C 6 - x y - 2 cách chọn.
Vậy có: C 6 x C 6 - x y - 2 cách chọn tập con thỏa mãn.
Ta có điều kiện:
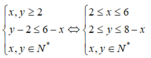
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:
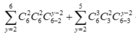
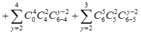
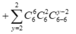
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: 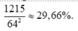

Đáp án C
Số tập con của A là 2 6
Số tập con gồm đúng 2 phần tử của A là C 6 2
Xác suất cần tính bằng C 6 2 2 6 = 15 64

1/ Số cách chọn 4 học sinh bất kì: \(C_{12}^4\)
Số cách chọn 4 học sinh có mặt đủ 3 lớp:
\(C_5^2.C_4^1.C_3^1+C_5^1.C_4^2.C_3^1+C_5^1.C_4^1.C_3^2\)
Số cách chọn thỏa mãn yêu cầu:
\(C_{12}^4-\left(C_5^2.C_4^1.C_3^1+C_5^1.C_4^2.C_3^1+C_5^1.C_4^1.C_3^2\right)\)
2/ Số tập con có 2 phần tử: \(C_n^2\)
Số tập con có 4 phần tử: \(C_n^4\)
\(C_n^4=20C_n^2\Leftrightarrow\frac{n!}{\left(n-4\right)!.4!}=\frac{20n!}{\left(n-2\right)!.2!}\)
\(\Leftrightarrow\left(n-2\right)\left(n-3\right)=\frac{20.4!}{2!}=240\)
\(\Leftrightarrow n^2-5n-234=0\Rightarrow n=18\)
3/ Từ 10 chữ số {0;1;...;9} có \(C_{10}^3\) cách chọn bộ 3 số tự nhiên phân biệt
Với mỗi bộ số có duy nhất 1 cách sắp xếp thỏa mãn \(a>b>c\)
Vậy có \(C_{10}^3\) chữ số thỏa mãn

Chọn C
Lời giải. Số tập con có 7 phần tử của tập A là C n 7
số tập con có 3 phần tử của tập A là C n 3
Theo giả thiết, ta có
C n 7 = 2 C n 3 → n = 11

Đáp án C
Điều kiện: n ≥ 7
Số tập con có 7 phân tử và 3 phân tử của A là C n 7 và C n 3
Suy ra
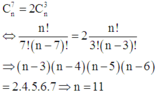
Số tập con có hai phần tử của A là: \(C_{90}^2=4005\)
Không gian mẫu: chọn 2 tập từ 4005 tập có \(C_{4005}^2\) cách
Trung bình cộng cách phần tử trong mỗi tập bằng 30 \(\Rightarrow\) tổng 2 phần tử của mỗi tập là 60
Ta có các cặp (1;59); (2;58);...;(29;31) tổng cộng 29 cặp (đồng nghĩa 29 tập thỏa mãn)
Chọn 2 tập từ 29 tập trên có \(C_{29}^2\) cách
Xác suất: \(P=\dfrac{C_{29}^2}{C_{4005}^2}=A\)