Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C
Ta tìm số cặp số (a;b) thoả mãn
![]()
![]()
Có 49 cặp (a;b) thỏa mãn. Do đó S gồm 49 phần tử:
Ta tìm số cặp (a;b) thoả mãn
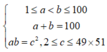
![]()
Do đó 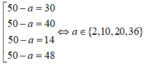
Vậy có 4 cặp số (a;b)có tổng bằng 100 và tích của chúng là một số chính phương.

- Có 5 cách chọn chữ số hàng trăm.
- Có 5 cách chọn chữ số hàng chục.
- Có 4 cách chọn chữ số hàng đơn vị.
Số số được tạo thành là:
\(5.5.4=100\) (số)
Tuy nhiên trong 100 số này đã bị mất đi 1 số số chẵn:
| 012 | 013 | 014 | 015 |
| 021 | 023 | 024 | 025 |
| 031 | 032 | 034 | 035 |
| 041 | 042 | 043 | 045 |
| 051 | 052 | 053 | 054 |
Vậy số số lẻ hơn số số chẵn là 8 số.
Có số số chẵn là:
\(\left(100-8\right):2=46\) (số)
Có số số lẻ là :
\(100-46=54\) (số)
Nếu coi 100 số là 100 %.
Xác xuất chọn được số chẵn ở lần chọn đầu là:
\(46:100.100=46\%\)
Xác xuất chọn được số chẵn ở lần chọn thứ 2 (nếu lần ko trúng) là:
\(46:99.100\approx46,5\)

Đáp án C
Số tập con của A là 2 6
Số tập con gồm đúng 2 phần tử của A là C 6 2
Xác suất cần tính bằng C 6 2 2 6 = 15 64

Số tập hợp con có k phần tử của tập hợp A (có 18 phần tử)
\(C_{18}^k\left(k=1,.....,18\right)\)
Để tìm max \(C_{18}^k,k\in\left\{1,2,.....,18\right\}\) (*), ta tiến hành giải bất phương trình sau :
\(\frac{C_{18}^k}{C_{18}^{k+1}}< 1\)
\(\Leftrightarrow C_{18}^k< C_{18}^{k+1}\)
\(\Leftrightarrow\frac{18!}{\left(18-k\right)!k!}< \frac{18!}{\left(17-k\right)!\left(k+1\right)!}\)
\(\Leftrightarrow\left(18-k\right)!k!>\left(17-k\right)!\left(k+1\right)!\)
\(\Leftrightarrow17>2k\)
\(\Leftrightarrow k< \frac{17}{2}\)
Điều kiện (*) nên k = 1,2,3,.....8
Suy ra \(\frac{C_{18}^k}{C_{18}^{k+1}}>1\) khi k = 9,10,...,17
Vậy ta có
\(C^1_{18}< C_{18}^2< C_{18}^3< .........C_{18}^8< C_{18}^9>C_{18}^{10}>.....>C_{18}^{18}\)
Vậy \(C_{18}^k\) đạt giá trị lớn nhất khi k = 9. Như thế số tập hợp con gồm 9 phần tử của A là số tập hợp con lớn nhất.
Chọn B
Số tập con của S là 2 6 = 64
Mỗi người có 64 cách chọn tập con, do vậy số phần tử của không gian mẫu là: 64 2
Ta tìm số cách chọn tập con thỏa mãn yêu cầu:
Giả sử tập con của A và B chọn được lần lượt có x,y phần tử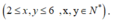
Khi đó: A có C 6 x cách chọn tập con, lúc này S còn 6 - x phần tử.
Ta chọn ra 2 phần tử gọi là a,b từ x phần tử trong tập con của A để xuất hiện trong tập con của B, có C x 2 cách.
Như vậy, tập con của B đã có 2 phần tử chung với tập con của A là a,b ta cần chọn thêm (y-2) phần tử khác trong (6-x) phần tử còn lại sau khi A đã chọn tập con,ở bước này có C 6 - x y - 2 cách chọn.
Vậy có: C 6 x C 6 - x y - 2 cách chọn tập con thỏa mãn.
Ta có điều kiện:
Cho x nhận các giá trị từ 2 đến 6, số cách chọn tập con thỏa mãn yêu cầu đề bài là:
= 240 + 480 + 360 + 120 + 15 = 1215
Xác suất cần tính bằng: