Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

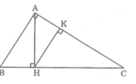
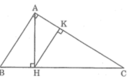
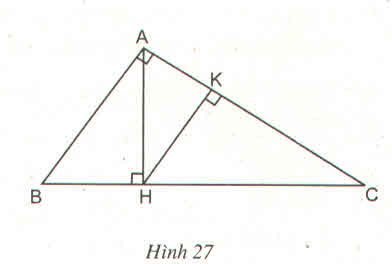
Trong hình trên có 5 tam giác đồng dạng với nhau theo từng đôi một đó là: △ ABC; △ HBA; △ HAC; △ KAH; △ KHC.

a) Xét ΔABC vuông tại A và ΔHAC vuông tại H có
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔHAC(g-g)
b) Xét tứ giác AKHI có
\(\widehat{KAI}=90^0\)
\(\widehat{HIA}=90^0\)
\(\widehat{HKA}=90^0\)
Do đó: AKHI là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)
c) Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HI là đường cao ứng với cạnh huyền AB, ta được:
\(AI\cdot AB=AH^2\)(1)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HK là đường cao ứng với cạnh huyền AC, ta được:
\(AK\cdot AC=AH^2\)(2)
Từ (1) và (2) suy ra \(AI\cdot AB=AK\cdot AC\)

a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
b: BC=10cm
AH=4,8cm
c: Xét ΔABH vuông tại H có HM là đườg cao
nên \(AM\cdot AB=AH^2\left(1\right)\)
Xét ΔACH vuông tại H có HN là đường cao
nên \(AN\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AM\cdot AB=AN\cdot AC\)
hay AM/AC=AN/AB
Xét ΔAMN vuông tại A và ΔACB vuông tại A có
AM/AC=AN/AB
Do đó: ΔAMN\(\sim\)ΔACB
\(a)\) Xét \(\Delta ABC\) và \(\Delta HBA:\)
\(\widehat{BAC}=\widehat{BHA}\left(=90^o\right).\\ \widehat{ABC}chung.\\ \Rightarrow\Delta ABC\sim\Delta HBA\left(g-g\right).\)
\(b)\) Xét \(\Delta ABC\) vuông tại A:
\(+)BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=6^2+8^2=36+64=100.\\ \Rightarrow BC=10\left(cm\right).\)\(+)AH.BC=AB.AC\) (Hệ thức lượng).\(\Rightarrow AH.10=6.8.\\ \Rightarrow AH=4,8\left(cm\right).\)\(c)\) Xét \(\Delta ABH\) vuông tại H, đường cao MH:\(AH^2=AM.AB\) (Hệ thức lượng). \(\left(1\right)\)Xét \(\Delta ACH\) vuông tại H, đường cao NH:\(AH^2=AN.AC\) (Hệ thức lượng). \(\left(2\right)\)Từ \(\left(1\right);\left(2\right)\Rightarrow AM.AB=AN.AC.\)Xét \(\Delta ACB\) và \(\Delta AMN:\)\(\Rightarrow\dfrac{AB}{AN}=\dfrac{AC}{AM}.\)\(\widehat{A}chung.\\ \dfrac{AB}{AN}=\dfrac{AC}{AM}\left(cmt\right).\\ \Rightarrow\Delta ACB\sim\Delta AMN\left(c-g-c\right).\)
Các cặp tam giác đồng dạng với nhau theo thứ tự các đỉnh tương ứng và viết tỉ lệ thức giữa các cặp cạnh tương ứng của chúng:
-
△
ABC đồng dạng
△
HBA. Ta có: 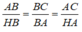
-
△
ABC đồng dạng
△
HAC. Ta có: 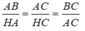
-
△
ABC đồngdạng
△
KHC. Ta có: 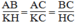
-
△
ABC đồng dạng
△
KAH. Ta có: 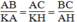
-
△
HBA đồng dạng
△
HAC. Ta có: 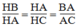
-
△
HBA đồng dạng
△
KHC. Ta có: 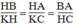
-
△
HBA đồng dạng
△
KAH. Ta có: 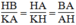
-
△
HAC đồng dạng
△
KHC.Ta có: 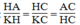
-
△
HAC đồng dạng
△
KAH. Ta có: 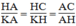
-
△
KHC đồngdạng
△
KAH. Ta có: 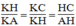

ΔAHB vuông tại H có HE vuông góc AB
nên AH^2=AE*AB
ΔAHC vuông tại H có HD vuông góc AC
nên AH^2=AD*AC
=>AE*AB=AD*AC
=>AE/AC=AD/AB
=>ΔAED đồng dạng với ΔACB
=>góc AED=góc ACB
=>góc BED+góc BCD=180 độ
=>góc CDE+góc B=180 độ