Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔOCA và ΔOBD có
OC/OB=OA/OD
\(\widehat{COA}=\widehat{BOD}\)
Do đó;ΔOCA\(\sim\)ΔOBD
Suy ra: \(\widehat{OCA}=\widehat{OBD}\)
hay AC//BD
=>ACDB là hình thang

a: Xét ΔOAB và ΔOCD có
OA=OC
\(\widehat{AOB}=\widehat{COD}\)
OB=OD
Do đó: ΔOAB=ΔOCD
b: ta có: ΔOAB=ΔOCD
nên \(\widehat{OAB}=\widehat{OCD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Xét tứ giác ABCD có AB//CD
nên ABCD là hình thang

Bài 5:
Xét ΔBAC có BA=BC
nên ΔBAC cân tại B
Suy ra: \(\widehat{BAC}=\widehat{BCA}\)
mà \(\widehat{BAC}=\widehat{ACD}\)
nên \(\widehat{ACB}=\widehat{ACD}\)
hay CA là tia phân giác của \(\widehat{BCD}\)

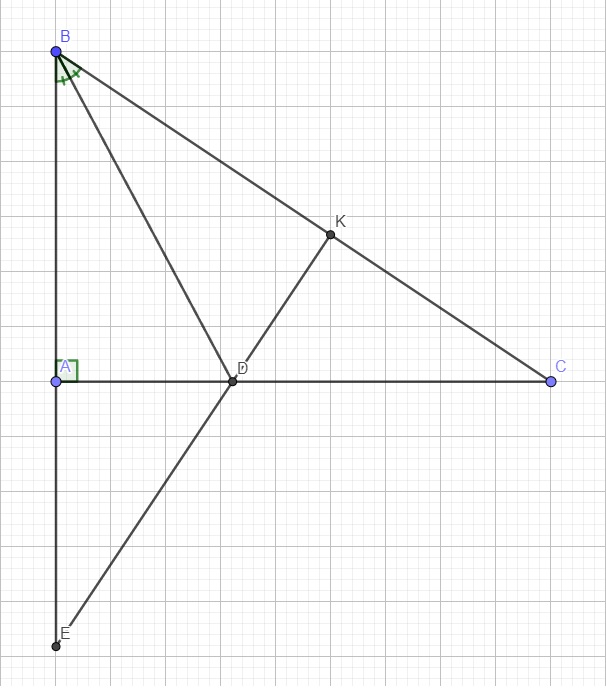
a.
Xét \(\Delta BAD\) và \(\Delta BKD\) có:
\(\left\{{}\begin{matrix}BA=BK\left(gt\right)\\\widehat{ABD}=\widehat{KBD}\left(gt\right)\\BD\text{ chung}\end{matrix}\right.\) \(\Rightarrow\Delta BAD=\Delta BKD\left(c.g.c\right)\)
\(\Rightarrow AD=DK\)
b.
Cũng do \(\Delta BAD=\Delta BKD\Rightarrow\widehat{BKD}=\widehat{BAD}\)
Mà \(\widehat{BAD}=90^0\left(gt\right)\Rightarrow\widehat{BKD}=90^0\)
\(\Rightarrow DK\perp BC\)
\(\Rightarrow\widehat{ABK}=\widehat{CDK}\) (cùng phụ \(\widehat{ACB}\))
c.
Xét hai tam giác ADE và KDC có:
\(\left\{{}\begin{matrix}AD=DK\left(cmt\right)\\\widehat{ADE}=\widehat{KDC}\left(\text{đối đỉnh}\right)\\DE=DC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow\Delta ADE=\Delta KDC\left(c.g.c\right)\)
\(\Rightarrow\widehat{DAE}=\widehat{DKC}=90^0\)
\(\Rightarrow\widehat{BAE}=\widehat{BAC}+\widehat{DAE}=90^0+90^0=180^0\)
\(\Rightarrow B,A,E\) thẳng hàng
Xét ΔOAC và ΔODB có
\(\dfrac{OA}{OD}=\dfrac{OC}{OB}\)
\(\widehat{AOC}=\widehat{DOB}\)
Do đó: ΔOAC\(\sim\)ΔODB
Suy ra: \(\widehat{OCA}=\widehat{OBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Xét tứ giác ABDC có AC//BD
nên ABDC là hình thang