Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Bài 2:
a: H là trung điểm của BC
nên HB=HC=2,5(cm)
⇔AH=5√152(cm)
⇔AH=5152(cm)
S=5√152⋅52=25√154(cm2)
S=5152⋅52=25154(cm2)
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
mà ˆB=ˆCB^=C^
nên BMNC là hình thang cân
Thu gọn

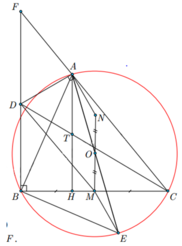
b) CD đi qua trung điểm của đường cao AH của D ABC
· Gọi F là giao của BD và CA.
Ta có BD.BE= BA.BM (cmt)
= > B D B A = B M B E = > Δ B D M ~ Δ B A E ( c − g − c ) = > B M D = B E A
Mà BCF=BEA(cùng chắn AB)
=>BMD=BCF=>MD//CF=>D là trung điểm BF
· Gọi T là giao điểm của CD và AH .
DBCD có TH //BD = > T H B D = C T C D (HQ định lí Te-let) (3)
DFCD có TA //FD = > T A F D = C T C D (HQ định lí Te-let) (4)
Mà BD= FD (D là trung điểm BF ) (5)
· Từ (3), (4) và (5) suy ra TA =TH ÞT là trung điểm AH .

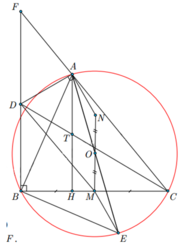
a) Chứng minh BA . BC = 2BD . BE
· Ta có: DBA+ ABC = 900 , EBM +ABC = 900
Þ DBA =EBM (1)
· Ta có: DONA = DOME (c-g-c)
Þ EAN= MEO
Ta lại có: DAB +BAE+ EAN = 900, và BEM +BAE +MEO = 900
Þ DAB= BEM (2)
· Từ (1) và (2) suy ra DBDA đồng dạng DBME (g-g)
= > B D B M = B A B E = > D B . B E = B A . B M = B A . B C 2 = > 2 B D . B E = B A . B C

a, Vì CM là tiếp tuyến của (A)
=> \(CM\perp AM\)
=> ^CMA = 90o
=> M thuộc đường tròn đường kính AC
Vì ^CHA = 90o
=> H thuộc đường tròn đường kính AC
Do đó : M và H cùng thuộc đường tròn đường kính AC
hay 4 điểm A,C,M,H cùng thuộc đường tròn đường kính AC
b, Vì AM = AH ( Bán kính)
CM = CH (tiếp tuyến)
=> AC là trung trực MH
=> \(AC\perp MH\)tại I
Xét \(\Delta\)AMC vuông tại M có MI là đường cao
\(\Rightarrow MA^2=AI.AC\)(Hệ thức lượng)
c, Vì CM , CH là tiếp tuyến của (A)
=> AC là phân giác ^HAM
=> ^HAC = ^MAC
Mà ^HAC + ^HAB = 90o
=> ^MAC + ^HAB = 90o
Ta có: ^BAD + ^BAC + ^CAM = 180o (Kề bù)
=> ^BAD + 90o + ^CAM = 180o
=> ^BAD + ^CAM = 90o
Do đó ^BAD = ^BAH (Cùng phụ ^CAM)
Xét \(\Delta\)BAD và \(\Delta\)BAH có:
AB chung
^BAD = ^BAH (cmt)
AD = AH (Bán kính (A) )
=> \(\Delta BAD=\Delta BAH\left(c.g.c\right)\)
=> ^ADB = ^AHB = 90o
\(\Rightarrow BD\perp AD\)
=> BD là tiếp tuyến của (A)
Làm đc đến đây thôi :(