Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Xét ΔMHN vuông tại H có
\(\sin N=\dfrac{MH}{MN}\)
nên \(MN=\dfrac{16\sqrt{3}}{3}\left(cm\right)\)
=>\(MP=16\left(cm\right)\)
\(S=8\cdot\dfrac{16\sqrt{3}}{3}=\dfrac{128\sqrt{3}}{3}\left(cm^2\right)\)

\(NP=4,5+6=10,5\left(cm\right)\)
Áp dụng tích chất đường phân giác:
\(\frac{MN}{NE}=\frac{MP}{EP}\Leftrightarrow\frac{MN}{4,5}=\frac{MP}{6}\Leftrightarrow MN=\frac{3}{4}MP\).
Áp dụng định lí Pythagore:
\(NP^2=MP^2+MN^2\)
\(\Leftrightarrow10,5^2=MP^2+\left(\frac{3}{4}MP\right)^2\Leftrightarrow MP=8,4\Rightarrow MN=6,3\)
\(MH=\frac{MN.MP}{NP}=\frac{8,4.6,3}{10,5}=5,04\)
\(NH=\frac{MN^2}{NP}=\frac{6,3^2}{10,5}=3,78\)
\(HE=NE-NH=4,5-3,78=0,72\)
\(S_{MHE}=\frac{1}{2}.MH.HE=\frac{1}{2}.0,72.5,04=1,8144\left(cm^2\right)\)

a: Xét ΔMNP vuông tại M có
\(\sin\widehat{N}=\dfrac{MP}{PN}=\dfrac{4}{5}\)
\(\cos\widehat{N}=\dfrac{MN}{MP}=\dfrac{3}{5}\)
\(\tan\widehat{N}=\dfrac{MP}{MN}=\dfrac{4}{3}\)
\(\cot\widehat{N}=\dfrac{MN}{MP}=\dfrac{3}{4}\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔMNP vuông tại M có MH là đường cao ứng với cạnh huyền NP, ta được:
\(\left\{{}\begin{matrix}MH\cdot NP=MN\cdot MP\\MN^2=HN\cdot NP\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}MH=2.4cm\\NH=1.8cm\end{matrix}\right.\)

Sửa đề: MP=24cm
NP=căn 18^2+24^2=30cm
NH=MN^2/NP=18^2/30=324/30=10,8cm
MH=18*24/30=14,4cm

(Tự vẽ hình)
- Xét △MNP vuông tại M, áp dụng định lí Pytago:
\(^{NM^2}\)+\(MP^2\)=\(NP^2\)
=\(72^2\)+\(96^2\)=\(NP^2\)
⇔\(NP^2\)=\(72^2\)+\(96^2\)=14400
⇔\(NP\)=\(\sqrt{14400}\)=120cm
- Xét △MNP vuông tại M, đường cao MH, theo hệ thức lượng ta có:
\(MN^2\)=\(NH.NP\)
\(72^2\)=\(NH.120\)
⇔\(NH\)=\(\dfrac{72^2}{120}\)=43,2 cm
- \(MH.NP\)=\(MP.MN\)
⇔ \(MH\)=\(\dfrac{MP.MN}{NP}\)=\(\dfrac{96.72}{120}\)=3,6cm

b: Xét ΔPDM vuông tại P có PH là đường cao ứng với cạnh huyền MD, ta được:
\(MH\cdot MD=MP^2\left(1\right)\)
Xét ΔMNP vuông tại M có MH là đường cao ứng với cạnh huyền NP, ta được:
\(PH\cdot PN=MP^2\left(2\right)\)
Từ (1) và (2) suy ra \(MH\cdot MD=PH\cdot PN\)


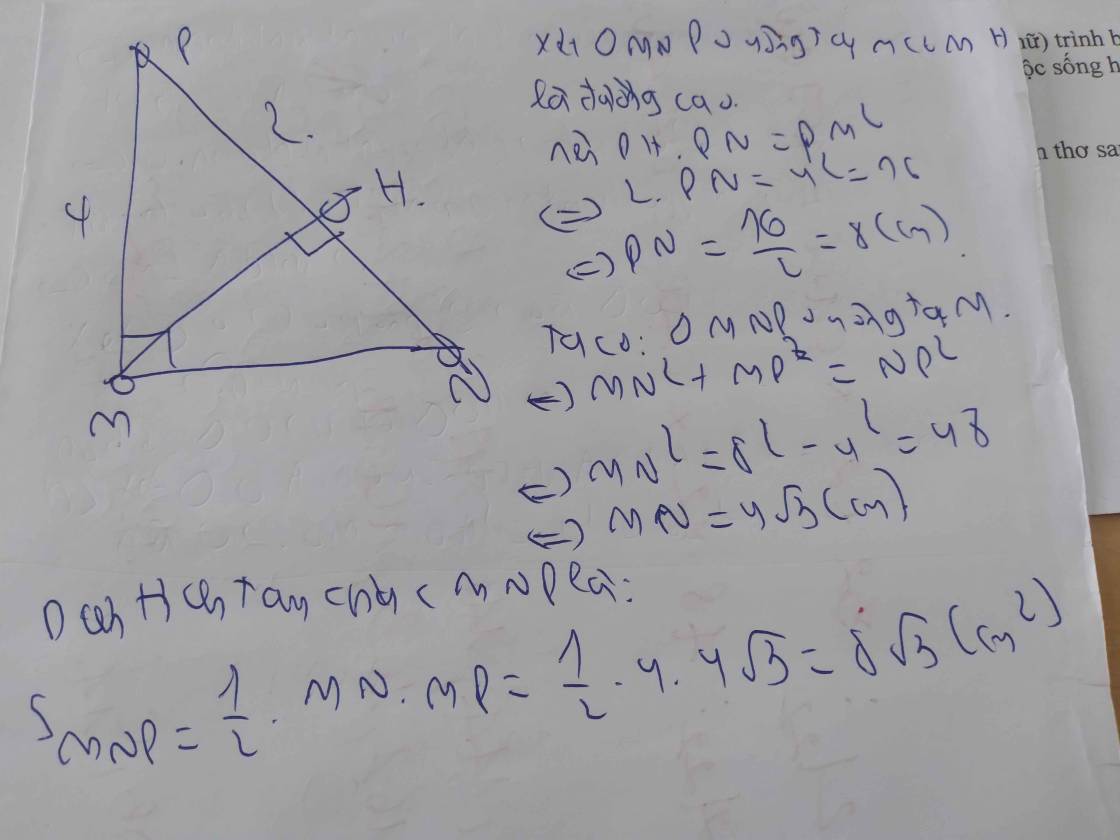
Áp dụng hệ thức lượng trong tam giác vuông vào ΔNMP vuông tại M có MH là đường cao ứng với cạnh huyền NP, ta được:
\(MH^2=HN\cdot HP\)
\(\Leftrightarrow HP=\dfrac{2.4^2}{1.8}=3.2\left(cm\right)\)
Diện tích tam giác MNP là:
\(S_{MNP}=\dfrac{MH\cdot NP}{2}=\dfrac{2.4\cdot5}{2}=6\left(cm^2\right)\)
Áp dụng hệ thức trong tam giác vuông:
`MH^2 =NH.PH`
`=>PH=MH^2 : NH = 2,4^2 : 1,8=3,2(cm)`
`=> NP=NH+PH=5(cm)`
`=> S= 1/2 . MH .NP =6(cm^2)`