Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: 5\(\widehat{M}\) = 3\(\widehat{N}\) => \(\frac{\widehat{M}}{3}\) = \(\frac{\widehat{N}}{5}\) => \(\frac{7\widehat{M}}{21}\) = \(\frac{4\widehat{N}}{20}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{7\widehat{M}}{21}\) = \(\frac{4\widehat{N}}{20}\) = \(\frac{7\widehat{M}-4\widehat{N}}{21-20}\) = 15o
Do \(\frac{7\widehat{M}}{21}\) = 15 => \(\widehat{M}\) = 45
\(\frac{4\widehat{N}}{20}\) = 15 => \(\widehat{N}\) = 75
Áp dụng tính chất tổng 3 góc trong 1 tam giác ta có:
\(\widehat{M}\) + \(\widehat{N}\) + \(\widehat{P}\) = 180 độ
=> 45 + 75 + \(\widehat{P}\) = 180
=> \(\widehat{P}\) = 60o
Vậy \(\widehat{P}\) = 60o.

a)
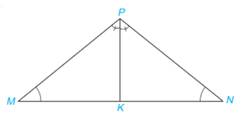
Xét tam giác MPK có:
\(\widehat {PKM} + \widehat {MPK} + \widehat {KMP} = {180^o}\)
Xét tam giác NPK có:
\(\widehat {PKN} + \widehat {NPK} + \widehat {KNP} = {180^o}\)
Mà \(\widehat {KMP} = \widehat {KNP};\,\,\,\widehat {MPK} = \widehat {NPK}\)
Suy ra \(\widehat {MKP} = \widehat {NKP}\).
b)Xét hai tam giác MPK và NPK có:
\(\widehat {MPK} = \widehat {NPK}\)
PK chung
\(\widehat {MKP} = \widehat {NKP}\)
=>\(\Delta MPK = \Delta NPK\)(g.c.g)
c) Do \(\Delta MPK = \Delta NPK\) nên MP=NP (2 cạnh tương ứng)
=> Tam giác MNP cân tại P.

a)
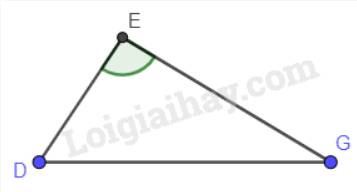
Trong tam giác DEG có góc E là góc tù (góc > 90°). Mà DG là cạnh đối diện với góc E nên DG là cạnh lớn nhất trong tam giác.
Vậy DE < DG.
b)

Tam giác MNP có \(\widehat M = 56^\circ \), \(\widehat N = 65^\circ \). Mà tổng ba góc trong một tam giác bằng 180°. Vậy \(\widehat P = 180^\circ - 56^\circ - 65^\circ = 59^\circ \).
Ta thấy: \(\widehat M < \widehat P < \widehat N\). Hay cạnh nhỏ nhất của tam giác MNP là NP (đối diện với góc M), cạnh lớn nhất của tam giác MNP là MP (đối diện với góc N).

Vì \(\widehat{MIN};\widehat{MIP}\) lần lượt là góc ngoài tg MIP và NIM nên
\(\widehat{MIP}-\widehat{MIN}=\widehat{IMN}+\widehat{N}-\widehat{IMP}-\widehat{P}==\widehat{N}-\widehat{P}\left(\widehat{IMN}=\widehat{IMP}\right)\)


Tam giác ABC và tam giác MNP bằng nhau (có ba cặp cạnh bằng nhau: AB = MN, BC = NP, AC = MP). Nên các cặp góc tương ứng trong hai tam giác này bằng nhau: \(\widehat A = \widehat M,\widehat B = \widehat N,\widehat C = \widehat P\).
Vậy \(\widehat A = \widehat M = 65^\circ \); \(\widehat B = \widehat N = 71^\circ \); \(\widehat C = \widehat P = 180^\circ - 65^\circ - 71^\circ = 44^\circ \)(vì tổng ba góc trong một tam giác bằng 180°).
tui làm rồi đó