Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta thấy \(\widehat{AMN}=\widehat{ABH}+\frac{1}{2}\widehat{BHQ}=\widehat{ACH}+\frac{1}{2}\widehat{CHP}=\widehat{ANM}\). Suy ra \(\Delta AMN\) cân tại A.
b) Dễ thấy tứ giác BEFC và BQPC nội tiếp, suy ra \(\widehat{HEF}=\widehat{HCB}=\widehat{HPQ}\), suy ra EF || PQ
Hiển nhiên \(OA\perp PQ\). Do đó \(OA\perp EF.\)
c) Gọi MK cắt BH tại I, NK cắt CH tại J, HK cắt BC tại S.
Vì A,K là trung điểm hai cung MN của (AMN) nên AK là đường kính của (AMN)
Suy ra \(MK\perp AB,NK\perp AC\)hay MK || CH, NK || BH
Ta có \(\Delta BHQ~\Delta CHP\), theo định lí đường phân giác và Thales thì:
\(\frac{IH}{IB}=\frac{MQ}{MB}=\frac{NP}{NC}=\frac{JH}{JC}\). Suy ra IJ || BC
Cũng từ MK || CH, NK || BH suy ra HIKJ là hình bình hành hay HK chia đôi IJ
Do vậy HK chia đôi BC theo bổ đề hình thang. Vậy HK đi qua S cố định.

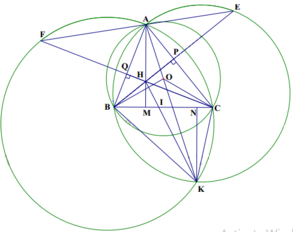
Ta có BOC=120o ;BKC =60o suy ra BOC +BKC =1800 nên tứ giác BOCK nội tiếp đường tròn.
Ta có OB=OC=R suy ra OB= OC=> BKO= CKO hay KO là phân giác góc BKC theo phần (a) KA

a) Đặt J là trung điểm cạnh BC. Theo quan hệ vuông góc giữa đường kính và dây ta có ^OIC = ^OJC = 900
Vậy I thuộc đường tròn đường kính OC cố định (đpcm).
b) Kẻ đường kính BK của (O). d cắt CK tại điểm S. Ta có AK vuông góc AB, IS vuông góc AB
Suy ra IS // AK. Vì I là trung điểm cạnh AC của tam giác AKC nên S là trung điểm CK cố định (đpcm).
c) OJ cắt (O) tại hai điểm phân biệt là A' và L (A' thuộc cung lớn BC). Hạ AH vuông góc BC
Ta thấy \(AH+JL\le AL\le2R=A'L\Rightarrow AH\le A'L-JL=A'J\)
Suy ra \(S=\frac{AH.BC}{2}\le\frac{A'J.BC}{2}\)(không đổi). Vậy S lớn nhất khi A trùng A'.
d) Trên đoạn JB,JC lấy M,N sao cho JM = JN = 1/6.BC. Khi đó M,N cố định.
Đồng thời \(\frac{JG}{JA}=\frac{JM}{JB}=\frac{JN}{JC}=\frac{1}{3}\). Suy ra ^MGN = ^BAC = 1/2.Sđ(BC (Vì GM // AB; GN // AC)
Vậy G là các điểm nhìn đoạn MN dưới một góc không đổi bằng 1/2.Sđ(BC, tức là một đường tròn cố định (đpcm).
Gọi I là tâm nội tiếp \(\Delta\)KLM. Ta sẽ chứng minh TI là phân giác ^LTM. Thật vây:
Kéo dài tia QT cho cắt \(\Omega\) tại điểm thứ hai là G. Đường thẳng MG và RQ cắt nhau ở V.
Do (S) tiếp xúc ngoài với \(\Omega\) nên Sđ(QT(S) = Sđ(MG\(\Omega\) => ^TRQ = ^TLG => ^TRQ = ^TMV
=> Tứ giác MVRT nội tiếp => ^MTV = ^MRV = ^KRQ = ^RQT hay ^GVT = ^GQV
=> \(\Delta\)GVT ~ \(\Delta\)GQV (g.g) => GV2 = GT.GQ. Tương tự: GF2 = GL2 = GT,GQ => GV=GF=GL
Kẻ tia đối Mx của ML thì ta có: ^xMV = ^GML = ^GFL = ^GLF (Vì GF=GL) = ^FMV => MV là phân giác ^FMx
Mặt khác: ^VFM = ^GFV - ^MFG = (1800 - ^FLM - 2.^MLG)/2 = (1800 - ^FLG - ^MLG)/2 = (^FML + ^FLM)/2
=> ^VFM = ^VFK/2 => FV là phân giác ^MFK. Từ đó: V là tâm bàng tiếp ứng đỉnh L của \(\Delta\)FLM
=> LV là phân giác ^MLF hay ^KLM => L,I,V thẳng hàng => ^MIV = (^KML+KLM)/2 = 900 - ^LKM/2 = ^MRV
Suy ra: Tứ giác MIRV nội tiếp. Kết hợp tứ giác MVRT nội tiếp => 5 điểm M,I,T,R,V cùng thuộc 1 đường tròn
=> Tứ giác MITV nội tiếp => ^MTI = ^MVI. Hoàn toàn tương tự, ta cũng có: ^LTI = ^LUI
Ta lại có: ^RVI = ^RMI = ^LMI => ^UVL = ^UML => Tứ giác LUVM nội tiếp => ^MVL = ^LUM hay ^MTI = ^LUI
Do đó: ^MTI = ^LTI. Vì vậy: TI là phân giác của ^LTM. Mà I cố định nên ta có ĐPCM.