Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Trên tia MA lấy điểm I sao cho MI=MC
Dễ thấy ΔCIMΔCIM đều ⇒MC=CI⇒MC=CI
Xét 2 tam giác ΔAICΔAICvàΔBMCvàΔBMC có
IC=MCIC=MC
∠IAC=∠MCB∠IAC=∠MCB (vì cùng cộng với ∠BCI=60∘∠BCI=60∘)
AC=BCAC=BC
Do đó ΔAICΔAIC = ΔBMCΔBMC
⇒AI=BM⇒AI=BM
⇒⇒ Đpcm
b) Dễ thấy ΔBAM∼ΔDCMΔBAM∼ΔDCM(g.g)
nên AMCM=BMDM⇒AM.DM=CM.BMAMCM=BMDM⇒AM.DM=CM.BM
⇒AMBM.CM=1MD⇒AMBM.CM=1MD
Áp dụng kết quả câu (a) ta có đpcm
c) Đặt MA=x, MB=y. Ta có
AM2+BM2+CM2=x2+y2+(x−y)2=2(x2+y2−xy)AM2+BM2+CM2=x2+y2+(x−y)2=2(x2+y2−xy) (1)
Kẻ BHBH vuông góc với AMAM
Do ∠BMH=60∘∠BMH=60∘ nên MH=y2,BH2=y2−(y2)2=3y24MH=y2,BH2=y2−(y2)2=3y24
do đó AB2=AH2+BH2=x2+y2−xyAB2=AH2+BH2=x2+y2−xy (2)
Từ (1) và (2) ⇒MA2+MB2+MC2=2AB2⇒MA2+MB2+MC2=2AB2 mà ΔABCΔABC đều
nên AB=R√3
k cho mình nha!!

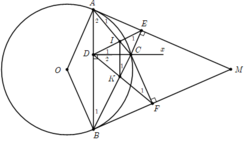
a, Xét tứ giác CDME có
^MEC = ^MDC = 900
mà 2 góc này kề, cùng nhìn cạnh MC
Vậy tứ giác CDME là tứ giác nt 1 đường tròn
b, bạn ktra lại đề

b. Do tứ giác MDBE nội tiếp (cmt) => \(\widehat{MBE}=\widehat{MBC}=\widehat{MDE}=\frac{1}{2}sđ\widebat{MC}\)(1)
Vì MD \(\perp\)AB tại D (gt) => \(\widehat{MDA}=90^o\)
MF \(\perp\)AC tại F (gt) => \(\widehat{MFA}=90^o\)
Xét tứ giác ADMF có: \(\widehat{MDA}+\widehat{MFA}=90^o+90^o=180^o\)=> tứ giác ADMF nội tiếp (dhnb)
=> \(\widehat{MDF}=\widehat{MAF}=\widehat{MAC}=\frac{1}{2}sđ\widebat{MC}\)(2)
Từ (1) và (2) => \(\widehat{MDE}=\widehat{MDF}\)=> D, E, F thẳng hàng (2 góc có cùng số đo, có 1 cạnh chung, 2 cạnh còn lại của 2 góc cùng nằm về 1 phía so với cạnh chung thì 2 cạnh còn lại trùng nhau)
* Ta có: tứ giác MEFC nội tiếp (cmt) => \(\widehat{EFM}=\widehat{ECM}=\frac{1}{2}sđ\widebat{EM}\)\(\Leftrightarrow\widehat{DFM}=\widehat{BCM}\)(3)
tứ giác MDBE nội tiếp (cmt) => \(\widehat{MDE}=\widehat{MBE}=\frac{1}{2}sđ\widebat{ME}\)\(\Leftrightarrow\widehat{MDF}=\widehat{MBC}\)(4)
Từ (3) và (4) => \(\Delta MDF\)đồng dạng với \(\Delta MBC\)(g.g) => \(\frac{MD}{MB}=\frac{MF}{MC}\Leftrightarrow MB\times MF=MD\times MC\)(đpcm)
c. Nối A với M, B với M
Ta có: \(\widehat{AMB}=\widehat{ACB}=\frac{1}{2}sđ\widebat{AB}\)(5)
Do tứ giác MEFC nội tiếp => \(\widehat{FME}=\widehat{FCE}=\frac{1}{2}sđ\widebat{EF}=\widehat{ACB}=\frac{1}{2}sđ\widebat{AB}\)(6)
Từ (5) và (6) => \(\widehat{AMB}=\widehat{FME}\)(7)
lại có: tứ giác ADMF nội tiếp (cmt) => \(\widehat{MAD}=\widehat{MFD}=\frac{1}{2}sđ\widebat{MD}\Leftrightarrow\widehat{MAB}=\widehat{MFE}\)(8)
từ (7) và (8) => \(\Delta ABM\)đồng dạng với \(\Delta FEM\)(g.g) => \(\frac{AB}{FE}=\frac{AM}{FM}\Leftrightarrow\frac{AB}{AM}=\frac{FE}{FM}\Leftrightarrow\frac{2\times AI}{AM}=\frac{2\times FK}{FM}\Leftrightarrow\frac{AI}{AM}=\frac{FK}{FM}\)(9)
Lại có: \(\widehat{MAD}=\widehat{MFD}\)(CMT) => \(\widehat{MAI}=\widehat{MFK}\)(10)
Từ (9) và (10) => \(\Delta MAI\)đồng dạng với \(\Delta MFK\)(c.g.c) => \(\widehat{IMA}=\widehat{KMF}\)(11)
Ta có: \(\widehat{MID}\)là góc ngoài tại đỉnh I của \(\Delta MAI\)=> \(\widehat{MID}=\widehat{MAI}+\widehat{IMA}\)
Tương tự: \(\widehat{MKD}\)là góc ngoài tại đỉnh K của \(\Delta MFK\)=> \(\widehat{MKD}=\widehat{MFK}+\widehat{KMF}\)
Từ (10) và (11) => \(\widehat{MID}=\widehat{MKD}\)=> Tứ giác MDIK là tứ giác nội tiếp (DHNB) => \(\widehat{IDM}+\widehat{IKM}=180^o\)(Hệ quả)
Mà \(\widehat{IDM}=\widehat{ADM}=90^o\)=> \(\widehat{IKM}=90^o\)<=> MK vuông góc với KI (ĐPCM)

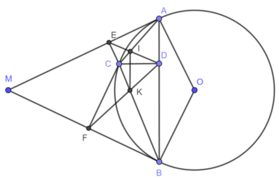
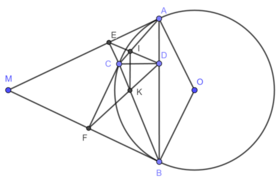
1) Hình vẽ câu 1) đúng
Ta có A E C ^ = A D C ^ = 90 0 ⇒ A E C ^ + A D C ^ = 180 0 do đó, tứ giác ADCE nội tiếp.
2) Chứng minh tương tự tứ giác BDCF nội tiếp.
Do các tứ giác A D C E , B D C F nội tiếp nên B 1 ^ = F 1 ^ , A 1 ^ = D 1 ^
Mà AM là tiếp tuyến của đường tròn (O) nên A 1 ^ = 1 2 s đ A C ⏜ = B 1 ^ ⇒ D 1 ^ = F 1 ^ .
Chứng minh tương tự E 1 ^ = D 2 ^ . Do đó, Δ C D E ∽ Δ C F D g.g
3) Gọi Cx là tia đối của tia CD
Do các tứ giác A D C E , B D C F nội tiếp nên D A E ^ = E C x ^ , D B F ^ = F C x ^
Mà M A B ^ = M B A ^ ⇒ E C x ^ = F C x ^ nên Cx là phân giác góc E C F ^ .
4) Theo chứng minh trên A 2 ^ = D 2 ^ , B 1 ^ = D 1 ^
Mà A 2 ^ + B 1 ^ + A C B ^ = 180 0 ⇒ D 2 ^ + D 1 ^ + A C B ^ = 180 0 ⇒ I C K ^ + I D K ^ = 180 0
Do đó, tứ giác CIKD nội tiếp ⇒ K 1 ^ = D 1 ^ mà D 1 ^ = B 1 ^ ⇒ I K / / A B

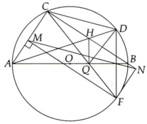
a, Tứ giác BDQH nội tiếp vì B D H ^ + B Q H ^ = 180 0
b, Vì tứ giác ACHQ nội tiếp =>
C
A
H
^
=
C
Q
H
^
Vì tứ giác ACDF nội tiếp => C A D ^ = C F D ^
Từ đó có C Q H ^ = C F D ^ mà 2 góc ở vị trí đồng vị => DF//HQ
c, Ta có H Q D ^ = H B D ^ (câu a)
H B D ^ = C A D ^ = 1 2 s đ C D ⏜
C A D ^ = C Q H ^ (ACHQ cũng nội tiếp)
=>
H
Q
D
^
=
H
Q
C
^
=> QH là phân giác
C
Q
D
^
Mặt khác chứng minh được CH là phân giác góc Q C D ^
Trong tam giác QCD có H là giao của ba đường phân giác nên H là tâm đường tròn nội tiếp => H cách đều 3 cạnh CD, CQ, DQ
d, Vì CMFN là hình chữ nhật nên MN và CF cắt nhau tại trung điểm của mỗi đường.
Trong tam giác FCD có MN//CD và MN đi qua trung điểm CF nên MN đi qua trung điểm DF
Mặt khác AB đi qua trung điểm của DF nên 3 đường thẳng MN, AB, DF đồng quy
bạn giải thích lại giúp mình câu b được không ạ? tại mình không hiểu câu đó lắm, mình cảm ơn!