Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

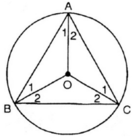
Vì tam giác ABC là tam giác đều nên 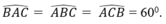
O tâm đường tròn ngoại tiếp tam giác ABC nên O là giao điểm 3 đường trung trực 3 cạnh- đồng thời O là giao điểm 3 đường phân giác của tam giác ABC
![]()
* Xét tam giác AOB có:
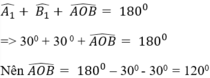
* Tượng tự ta được: ![]()
a) Ta có : ^A = ^B = ^C =60^o ( gt )
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của ba cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC
Nên ^A1 = ^A2 = ^B1 = ^B2 = ^C1 = ^C2 = 30^o
=> ^AOB = 180^o - ^A1 - ^B1 = 180^o - 30^o - 30^o = 120^o
Tương tự ta có : ^AOB = ^BOC = ^COA = 120^o
b) Từ ^AOB = ^BOC = ^COA = 120^o , ta có :
\(\Rightarrow sđ\widebat{AB}=sđ\widebat{CA}=sđ\widebat{CB}=120^o\)
\(\Rightarrow sđ\widebat{ABC}=sđ\widebat{BCA}=sđ\widebat{CAB}=360^o-120^o=240^o\)

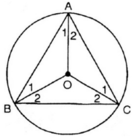
Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400

a: Xét ΔBAO vuông tại A có \(cosAOB=\dfrac{OA}{OB}=\dfrac{1}{\sqrt{2}}\)
=>\(\widehat{AOC}=45^0\)
=>\(sđ\left(OA;OC\right)=45^0\)
b: Số đo cung AC nhỏ là:
\(sđ\stackrel\frown{AC}=45^0\)
Số đo cung AC lớn là:
3600-450=3150

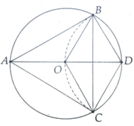
a, HS Tự chứng minh
b, Tính được C B D ^ = C B O ^ = O B A ^ = 30 0
c, Chứng minh ∆ABC cân tại A có: A B C ^ = 60 0 => ∆ABC đều

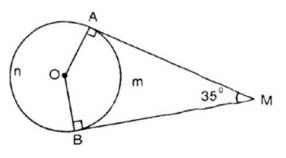
a) Trong tứ giác AOBM có 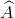 =
= 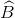 =
= 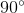 .
.
Suy ra cung AMB +  =
= 
=> cung AMB=  -
- 
=  -
- 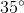
= 
b) Từ 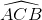 =
=  . Suy ra số đo cung nhỏ AB =
. Suy ra số đo cung nhỏ AB =  và số đo cung lớn AB :
và số đo cung lớn AB :
Cung AB = 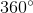 -
-  =
= 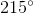
 Good luck~
Good luck~
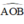
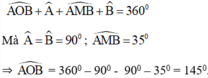
a) Ta có: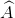 =
= 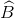 =
= 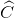 =
= 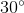 (gt)
(gt)
Suy ra: =
= 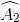 =
= 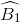 =
= 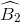 =
= 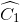 =
= 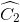 =
= 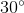 .
.
Tâm O của đường tròn ngoại tiếp tam giác là giao điểm của ba đường trung trực của bà cạnh cũng chính là giao điểm của ba đường phân giác của tam giác đều ABC.
Suy ra: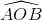 =
= 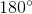 - (
- ( +
+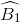 ) =
) = 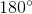 -
- 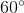 =
= 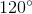
Tương tự ta suy ra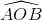 =
= 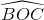 =
= 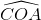 =
= 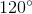 .
.
b) Từ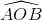 =
= 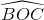 =
= 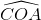 =
= 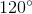 ta suy ra:
ta suy ra:
Cung ABC = BCA = CAB = 240º