Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án:
A) Xét ΔABD và ΔEBD có:
+) AB=BE (gt)
+) góc ABD= góc EBD (do BD là phân giác góc B)
+) BD chung
=> ΔABD = ΔEBD (c-g-c)
b)
Qua C kẻ đường thẳng vuông góc với BD tại H.
Xét ΔBCF có: BH là đường cao đồng thời là phân giác của góc B
=> ΔBCF cân tại B (tính chất)
=> BC= BF (điều phải chứng minh)
c)
Xét ΔABC và ΔEBF có:
+) AB = EB (gt)
+) góc B chung
+) BC= BF (câu b)
=> ΔABC = ΔEBF (c-g-c)
d)
Từ ý a, ΔABD = ΔEBD (c-g-c)
=> góc BAD= góc BED = 90
=> DE ⊥ BC
Xét ΔBCF có: BH và CA là 2 đường cao cắt nhau tại D
=> D là trực tâm
=> FD ⊥ BC
=> DE trùng với FD
=> D,E,F thẳng hàng

d: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>góc BKC=góc BCK

tu ve hinh :
cau b la vuong goc phai k
a, tamgiac ABC can tai A(gt) => AB = AC va goc ABC = goc ACB (dn)
goc ADB = goc ADC do AD | BC (GT)
=> tamgiac ADB = tamgiac ADC (ch - gn)
=> BD = DC (dn)
b, xet tamgiac BHD va tamgiac CKD co : BD = DC (Cau a)
goc ABC = goc ACB (cau a)
goc BHD = goc DKC = 90 do HD | AB va HK | AC (gt)
=> tamgiac BHD = tamgiac CKD (ch - gn)
=> HD = DK (dn)
c, xet tamgiac AHD va tamgiac AKD co : AD chung
HD = DK (cau b)
goc AHD = goc AKD = 90 do HD | AB va HK | AC (gt)
=> tamgiac AHD = tamgiac AKD (ch - cgv)
=> tamgiac AHK can tai A (dn)
=> goc AHK = (180 - goc BAC) : 2
tamgiac ABC can tai A (gt) => goc ABC = (180 - goc BAC) : 2
=> goc AHK = goc ABC 2 goc nay dong vi
=> HK // BC (tc)
d, tu ap dung py-ta-go

`@` `\text {dnammv}`
`a,`
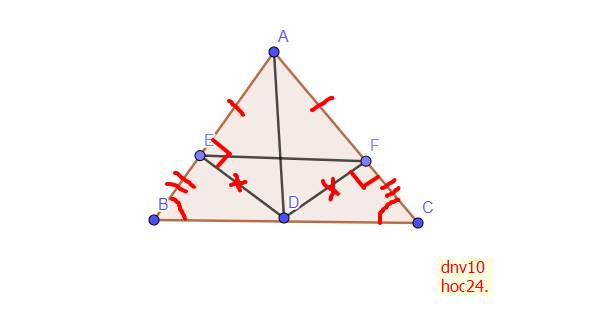
Xét \(\Delta BED\) và \(\Delta CFD\) có:
\(\left\{{}\begin{matrix}\text{BD = CD (D là trung điểm của BC}\\\widehat{\text{B}}=\widehat{\text{C}}\left(\text{ }\Delta\text{ABC cân tại A}\right)\\\widehat{BED}=\widehat{CFD}\left(=90^0\right)\end{matrix}\right.\)
`=> \Delta BED = \Delta CFD (ch-gn)`
`-> \text {BE = CF (2 cạnh tương ứng)}`
`b,`
Vì `\Delta BED = \Delta CFD (a)`
`-> \text {DE = DF (2 cạnh tương ứng)}`
`\text {Xét}` `\Delta DEF:`
`\text {DE = DF}`
`-> \Delta DEF` là `\Delta` cân
`c,`
Vì \(\left\{{}\begin{matrix}\text{AB = AC (tam giác ABC cân tại A)}\\\text{BE = CF (a)}\end{matrix}\right.\)
`-> \text {AE = AF}`
\(\text{Xét }\Delta\text{ AEF}: \)
`\text {AE = AF}`
`-> \Delta AEF` là `\Delta` cân (tại A).
`->`\(\widehat {AEF}= \widehat {AFE}\)\(=\dfrac{180-\widehat{A}}{2}\text{ }\left(1\right)\)
`\Delta ABC` cân tại `A`
`->`\(\widehat {ABC}= \widehat {ACB}=\)\(\dfrac{180-\widehat{A}}{2}\text{ }\left(2\right)\)
Từ `(1)` và `(2)`
`->`\(\widehat {AEF}= \widehat {ABC}\)
Mà `2` góc này nằm ở vị trí đồng vị
`-> \text {EF // BC (tính chất 2 đường thẳng //).}`

c) tam c/m được t/g ABC cân tại A
trong t/g cân thì đường phân giác xuất phát từ đỉnh trùng với đường trung tuyến nên DB=DC
t/g FDB=t/g EDC (cạnh huyền-góc nhọn)
=> DF=DE
d) có BF=EC (t/g FDB=t/g EDC)
và AB=AC (t/g ABC cân)
nên AB-BF=AC-EC
=> AF=AE
=> t/g AFE cân tại A
trong t/g cân thì đường phân giác xuất phát từ đỉnh trùng với đường cao nên AD vuông góc với EF
trong t/g cân thì đường phân giác xuất phát từ đỉnh trùng với đường cao nên AD vuông góc với BC (t/g ABC cân tại A)
ta có AD vuông góc với EF và BC nên EF//BC
