Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: MN là đường trung bình
nên MN//CD
mà CD\(\perp\)AH
nên AH\(\perp\)MN

Xét tam giác ACD có:
MN là đường trung bình
=> MN//CD
Mà AH⊥CD(AH là đường cao)
=> AH⊥MN(từ vuông góc đến song song)

Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{EAD}=90^0\)
Do đó: ADHE là hình chữ nhật
Suy ra: Hai đường chéo AH và DE cắt nhau tại trung điểm của mỗi đường
=>IA=IH
hay I nằm trên đường trung trực của AH

a: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến ứng với cạnh huyền AB
nên HM=AM=MB
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến ứng với cạnh AC
nên HN=AN=NC(3)
Ta có: MA=MH
nên M nằm trên đường trung trực của AH(1)
Ta có: NA=NH
nên N nằm trên đường trung trực của AH(2)
Từ (1) và (2) suy ra MN là đường trung trực của AH
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔABC
Suy ra: MN//BC
hay MN//HI
Xét ΔABC có
M là trung điểm của AB
I là trung điểm của BC
Do đó: MI là đường trung bình của ΔABC
Suy ra: \(MI=\dfrac{AC}{2}=AN=NC\left(4\right)\)
Từ (3) và (4) suy ra MI=HN
Xét tứ giác MNIH có MN//HI
nên MNHI là hình thang
mà MI=HN
nên MNHI là hình thang cân

Bạn vô câu hỏi tương tự nha , ở đó có cả phần a và phần b
Bài đó được giáo viên giải đấy
Chắc 100% lun !!!

Xét tứ giác AEHD, có:
∠A = ∠E = ∠D = 90°
=> tứ giác AEHD là hình chữ nhật.
O là giao điểm hai đường chéo hcn AEHD
=> OD = OH (1).
DI là đường trung tuyến ứng với cạnh huyền của Δ vuông DHB
=> DI = 1/2 BH = IH (2).
Xét Δ IDO và Δ IHO, có:
OD = OH (1).
OI là cạnh chung.
DI = IH (2).
=> Δ IDO = Δ IHO (đpcm).
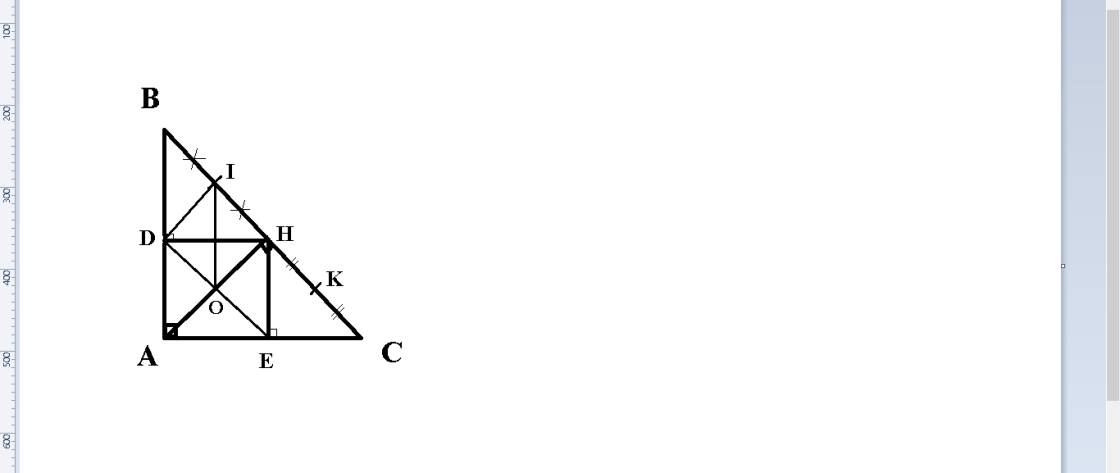
(bồ xem thử ổn hông nhe).

a:Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
=>ΔABC đồng dạng vớiΔHBA
b: ΔACB vuông tại A có AH là đường cao
nên AH^2=HB*HC
Ta có:MN là đường trung bình của ΔACD
⇒MN//CD
mà AH⊥CD(đường cao AH)
⇒AH⊥MN