Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

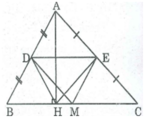
* Vì D trung điểm của AB (gt) và E trung điểm của AC (gt) nên DE là đường trung bình của tam giác ABC
⇒ DE // BC hay DE // HM
Suy ra tứ giác DEMH là hình thang
* Mà M trung điểm BC (gt) nên DM là đường trung bình của ∆ BAC
⇒ DM = 1/2 AC (tính chất đường trung bình của tam giác) (1)
* Trong tam giác vuông AHC có ∠ (AHC) = 90 0 . HE là đường trung tuyến ứng với cạnh huyền AC.
⇒ HE = 1/2 AC (tính chất tam giác vuông) (2)
Từ (1) và (2) suy ra: DM = HE
Vậy hình thang DEMH là hình thang cân (vì có 2 đường chéo DM và EH bằng nhau).

a: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC và \(MN=\dfrac{BC}{2}\)
mà E\(\in\)BC và \(BE=\dfrac{BC}{2}\)
nên MN//BE và MN=BE
Xét tứ giác BMNE có
MN//BE
MN=BE
Do đó: BMNE là hình bình hành
b: Ta có: ΔAHB vuông tại H
mà HM là đường trung tuyến ứng với cạnh huyền AB
nên HM=AM=MB
Ta có: ΔAHC vuông tại H
mà HN là đường trung tuyến ứng với cạnh huyền AC
nên HN=AN=NC
Ta có: HM=AM
nên M nằm trên đường trung trực của AH\(\left(1\right)\)
Ta có: HN=AN
nên N nằm trên đường trung trực của AH\(\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\) suy ra MN là đường trung trực của AH
b: Xét ΔBAC có
M là trung điểm của AB
E là trung điểm của BC
Do đó: ME là đường trung trực của ΔBAC
Suy ra: ME//AC và \(ME=\dfrac{AC}{2}\)
mà \(AN=\dfrac{AC}{2}\)
nên ME=AN
mà AN=HN
nên HN=ME
Xét tứ giác HMNE có
MN//HE
nên HMNE là hình thang
Hình thang HMNE có HN=ME
nên HMNE là hình thang cân

* Hình tự vẽ ạ :
a)
Ta có: M là trung điểm của BC => BM = MC mà BM = 3,5cm => MC = 3,5cm => BC = BM+MC = 3,5+3,5=7 (cm)
\(S_{\Delta ABC}=\dfrac{1}{2}AH.BC=19,25\left(cm^2\right)\)
b)
Tam giác ABC có:
+ E là trung điểm của AC (gt)
M là trung điểm của BC (gt)
=> ME là đường trung bình của tam giác ABC
=> ME // AB; ME = 1/2AB ( tính chất đường trung bình )
Ta lại có:
D là trung điểm của AB => AD = BD
mà ME=1/2AB (cmt)
=> ME=BD=AD
Tứ giác BDME có:
ME // BD ( ME // AB )
ME = BD (cmt)
=> tứ giác BDME là hình bình hành

Trả lời :
*Tự vẽ hình nhé b.
Xét \(\Delta ABC\)có : D là trung điểm AB, E là trung điểm AC
=> DE là đường trung bình \(\Delta ABC\)
=> DE // BC mà H, M \(\in BC\)=> DE // HM
=> DEMH là hình thang (1).
Xét \(\Delta ABC\)có : D là trung điểm AB, M là trung điểm BC
=> DM là đường trung bình \(\Delta ABC\)
=> \(DM=\frac{1}{2}AC\)(*).
\(\Delta\)vuông ACH có : \(\widehat{ACH}=90^o\), HE là trung tuyến
=> \(HE=\frac{1}{2}AC\)(**)
Từ (*) và (**) => DM = HE (2).
Từ (1) và (2) => DEMH là hình thang cân (đpcm).

a: Xét ΔBAC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình của ΔBAC
Suy ra: MN//BC
Xét tứ giác BMNC có MN//BC
nên BMNC là hình thang
b: Xét ΔABC có
M là trung điểm của AB
K là trung điểm của BC
Do đó: MK là đường trung bình của ΔBAC
Suy ra: MK//AC và \(MK=\dfrac{AC}{2}\)
mà N\(\in\)AC và \(AN=\dfrac{AC}{2}\)
nên AN//MK và AN=MK
Xét tứ giác AMKN có
AN//MK
AN=MK
Do đó: AMKN là hình bình hành

 Bạn tham khảo thử nhé, không hiểu thì cứ hỏi mình!
Bạn tham khảo thử nhé, không hiểu thì cứ hỏi mình!
+)Trong tam giác ABC có : D là trung điểm của AB , E là trung điểm của AC
=> DE là đường trung bình => DE // BC hay DE // HM
=> tứ giác DEMH là hình thang (1)
mk chỉ cm đc 1 ý thui ak , sr ha ^^