Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dựng đường thẳng qua B và song song với DK cắt AC tại G
Xét tam giác ADK ta có:
AB = BD; BG // DK
⇒ KG = GA = \(\dfrac{1}{2}\) AK (định lý 1 đường trung bình của tam giác) (1)
Xét tam giác BCG ta có:
BM = MC; MK // BG
⇒ KC = KG (định lý 1 đường trung bình của tam giác) (2)
Kết hợp (1) và (2) ta có:
KC = \(\dfrac{1}{2}\) AK
⇒ AK = 2KC (đpcm)

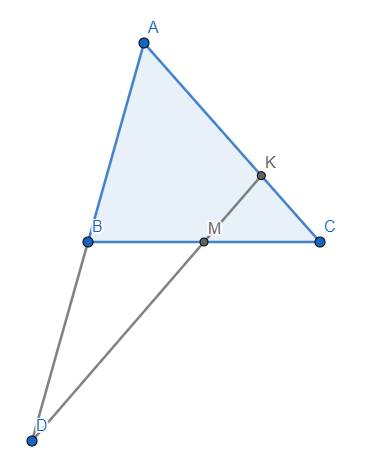
Bài này có thể giải bằng cách dùng định lý Menelaus khá ngắn như sau:
Áp dụng định lý Menelaus cho tam giác ABC với cát tuyến DMK, ta có: \(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{AB}=1\) \(\Rightarrow1.\dfrac{KC}{KA}.2=1\) \(\Leftrightarrow\dfrac{KC}{KA}=\dfrac{1}{2}\) \(\Leftrightarrow KA=2KC\) (đpcm)
Nhưng nếu bạn chưa được dùng định lý Menelaus thì sẽ phải làm như sau:
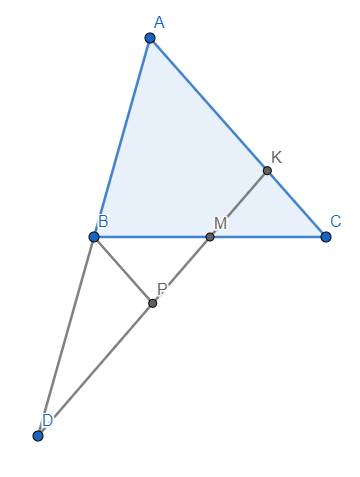
Kẻ BP//AC \(\left(P\in DK\right)\). Khi đó theo định lý Thales, \(\dfrac{MB}{MC}=\dfrac{BP}{CK}\) và \(\dfrac{DA}{DB}=\dfrac{AK}{BP}\). Do đó:
\(\dfrac{MB}{MC}.\dfrac{KC}{KA}.\dfrac{DA}{DB}=\dfrac{BP}{CK}.\dfrac{CK}{AK}.\dfrac{AK}{BP}=1\), và tới đây ta lại quay về tính như đã trình bày ở trên.

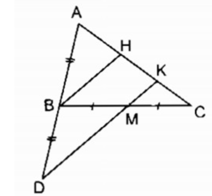
Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)

Gọi H là trung điểm của AK
Trong ∆ ADK ta có BH là đường trung bình của ∆ ADK.
⇒ BH // DK (tính chất đường trung bình của tam giác)
Hay BH // MK
Trong ∆ BCH ta có M là trung điểm của BC
MK // BH
⇒ CK = HK
AK = AH + HK = 2HK
Suy ra: AK = 2 KC ( vì HK =KC)

Qua B kẻ BH // AC , cắt DM tại H
Ta có \(\begin{cases}BH\text{//}AK\\AB=BD\end{cases}\) => BH là đường trung bình của tam giác ADK
=> AK=2BH (1)
Dễ dàng chứng minh được \(\Delta MKC=\Delta MBH\left(g.c.g\right)\)
=> BH = CK (2)
Từ (1) và (2) suy ra AK = 2CK

Qua B kẻ BH // AC , cắt DM tại H
Ta có {BH // AK ; AB = BD => BH là đường trung bình của tam giác ADK
=> AK=2BH (1)
Dễ dàng chứng minh được tam giác MKC = tam giác MBH (g.c.g)
=> BH = CK (2)
Từ (1) và (2) suy ra AK = 2CK

Qua B Kẻ BH // AC , cắt DM tại H
Ta có : BH // AK
AB // BD
=> BH là đường trung bình của tam giác ADK
=> AK = 2 BH (1)
· * Xét tam giác MKC và tam giác MBH .
CÓ : BM = CM ( M là trung điểm của BC)
Góc M1= Góc M2 ( 2 góc đối đỉnh)
Góc MKC = MBH ( = 90 *)* là độ
=> Tam giác MKC = Tam giác MBH ( g. c . g)
=> BH = KC ( 2 cạnh tương ứng )(2)
Từ (1), (2) suy ra được AK = 2 KC
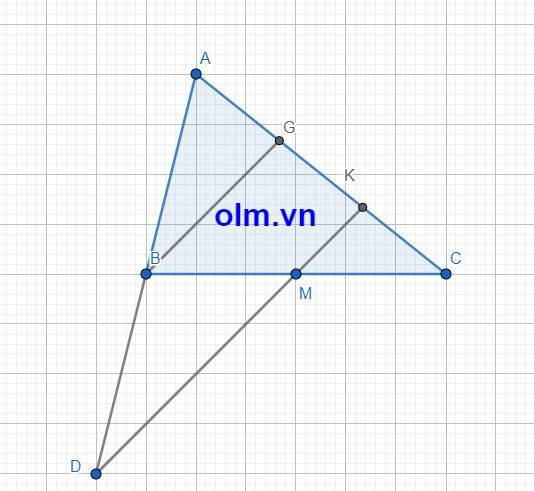
Qua B dựng đường thẳng song song với DK và cắt AC tại G
Xét tam giác ADK ta có: AB = BD; BG//DK
⇒ AG = GK (định lý đường trung bình của tam giâc)
⇒ GK = \(\dfrac{1}{2}\) AK (1)
Xét tam giác BCG ta có:
BM = MC; MK // BG
⇒ GK = KC (định lý 1 đường trung bình của tam giác) (2)
Kết hợp (1) và (2) ta có:
KC = \(\dfrac{1}{2}\) AK
⇒ AK = 2KC (đpcm)