Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{BC}=\left(-6;-3\right)\)
Trọng tâm của ΔABC là G(2; 1)
Khi tịnh tiến ΔABC thành ΔA'B'C' theo \(\overrightarrow{BC}=\left(-6;-3\right)\) thì G(2;1) cũng sẽ được tịnh tiến theo \(\overrightarrow{BC}=\left(-6;-3\right)\) thành G' (x;y)
⇒ \(\overrightarrow{GG'}=\overrightarrow{BC}\) = (-6 ; -3)
⇒ \(\left\{{}\begin{matrix}x-2=-6\\y-1=-3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-4\\y=-2\end{matrix}\right.\). Vậy G' (-4 ; -2)

Hướng dẫn:
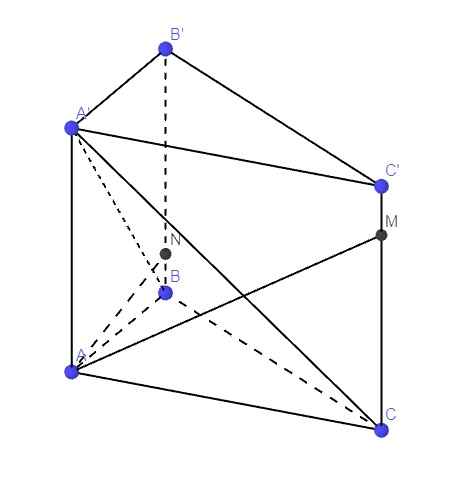
Dễ dàng nhận ra A thuộc B'G (vì AB' là đường chéo của hbh mặt bên nên là 1 trung tuyến)
Gọi M, M' lần lượt là trung điểm BC và B'C'
=> (GOB') là (AMB')
(CA'O') là (CA'M')
Có B'M'CM là hình bình hành
A'M'MA cũng là hbh
Suy ra 2 cặp đường thẳng song song và cắt nhau => đpcm

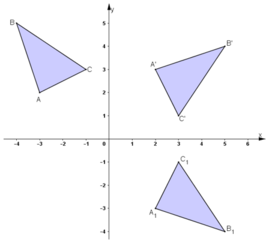
+ Chứng minh hoàn toàn tương tự ta được
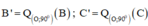
b. ΔA1B1C1 là ảnh của ΔABC qua phép dời hình có được bằng cách thực hiện liên tiếp phép quay tâm O góc –90º và phép đối xứng qua trục Ox.
⇒ ΔA1B1C1 là ảnh của ΔA’B’C’ qua phép đối xứng trục Ox.
⇒ A1 = ĐOx(A’) ⇒ A1(2; -3)
B1 = ĐOx(B’) ⇒ B1(5; -4)
C1 = ĐOx(C’) ⇒ C1(3; -1).
a) + Ta có:
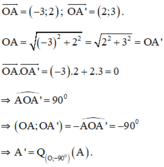

a.
\(\left\{{}\begin{matrix}BB'\perp\left(ABC\right)\Rightarrow BB'\perp BC\\AB\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(ABB'A'\right)\)
\(\Rightarrow BC=d\left(C;\left(A'AB\right)\right)\)
\(S_{A'AB}=\dfrac{1}{2}S_{ABB'A'}=\dfrac{3a^2}{2}\)
\(\Rightarrow V_{C.A'AB}=\dfrac{1}{3}BC.S_{A'AB}=\dfrac{1}{3}.2a.\dfrac{3a^2}{2}=a^3\)
b.
Theo cmt, \(BC\perp\left(ABB'A'\right)\Rightarrow BC\perp AN\)
Mà \(\left\{{}\begin{matrix}A'C\perp\left(P\right)\\AN\in\left(P\right)\end{matrix}\right.\) \(\Rightarrow AN\perp A'C\)
\(\Rightarrow AN\perp\left(A'BC\right)\Rightarrow AN\perp A'B\)
c.
Ta có: \(AA'||BB'\Rightarrow d\left(B;AA'\right)=d\left(N;AA'\right)\)
\(\Rightarrow S_{A'AN}=S_{A'AB}\)
Lại có: \(CC'||BB'\Rightarrow CC'||\left(ABB'A'\right)\)
\(\Rightarrow d\left(C';\left(ABB'A'\right)\right)=d\left(M;\left(ABB'A'\right)\right)\)
\(\Rightarrow V_{A'AMN}=V_{CA'AB}=a^3\)

Sao G và G' chẳng liên quan gì đến bài toán vậy ta?
Do tam giác ABC vuông tại B và M là trung điểm AC\(\Rightarrow M\) là tâm đường tròn ngoại tiếp tam giác ABC
Tương tự, N là tâm đường tròn ngoại tiếp tam giác A'B'C'
Mà \(MN//AA'\Rightarrow\left\{{}\begin{matrix}MN\perp\left(ABC\right)\\MN\perp\left(A'B'C'\right)\end{matrix}\right.\)
\(\Rightarrow\) với điểm P bất kì thuộc MN thì \(\left\{{}\begin{matrix}PA=PB=PC\\PA'=PB'=PC'\end{matrix}\right.\)
Gọi Q là trung điểm MN \(\Rightarrow QA=QA'\)
\(\Rightarrow QA=QB=QC=QA'=QB'=QC'\)
Vậy trung điểm của MN chính là điểm cách đều cách đỉnh của lăng trụ