Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

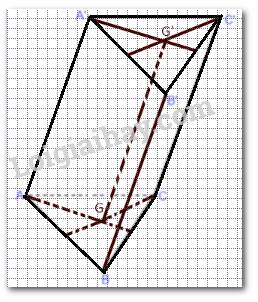
a) Ta có ABC.A'B'C' là hình lăng trụ nên \(\Delta ABC = \Delta A'B'C'\) suy ra AG = A'G'.
Lại có (ABC) // (A'B'C'), giao tuyến của mp(AGG'A') với (ABC) và (A'B'C') lần lượt là AG, A'G' suy ra AG // A'G'.
Như vậy , tứ giác AGG'A' có AG = A'G', AG // A'G' là hình bình hành.
b) AGG'A' là hình bình hành suy ta AA' // GG'.
Lại có AA' // CC' (do ABC.A'B'C' là hình lăng trụ).
Mặt phẳng (AGC) // (A'G'C') suy ra AGC.A'G'C' là hình lăng trụ.

a: ABCD.A'B'C'D là hình hộp chữ nhật
=>AA'//DD'//BB'//CC'
AA'//CC'
=>AA'//(CC'D'D)
B'B//D'D
=>B'B//(CC'D'D)
mà AA'//(CC'D'D)
và A'A và B'B cùng thuộc mp(AA'B'B)
nên (AA'B'B)//(CC'D'D)
b: Xét tứ giác ADC'B' có
AD//B'C'
AD=B'C'
Do đó: ADC'B' là hình bình hành
=>AB'//DC'
=>AB'//(C'BD)(1)
Xét tứ giác BDD'B' có
BB'//DD'
BB'=D'D
Do đó: BDD'B' là hình bình hành
=>BD//B'D'
=>B'D'//(C'BD)(2)
Từ (1) và (2) suy ra (C'BD)//(AB'D')
c: Gọi G là trọng tâm của ΔABC
Xét ΔBAC có
BO là đường trung tuyến
G là trọng tâm
Do đó: B,O,G thẳng hàng và \(BG=\dfrac{2}{3}BO\)
Gọi M là giao điểm của AG với BC; M' là giao điểm của A'G' với B'C'
Xét ΔABC có
G là trọng tâm
M là giao điểm của AG với BC
Do đó: M là trung điểm của BC và \(AG=\dfrac{2}{3}AM\)
Xét ΔA'B'C' có
G' là trọng tâm
A'G' cắt B'C' tại M'
Do đó: M' là trung điểm của B'C'
Xét ΔABM và ΔA'B'M' có
AB=A'B'
\(\widehat{ABM}=\widehat{A'B'M'}\)
BM=B'M'
Do đó: ΔABM=ΔA'B'M'
=>AM=A'M'
Xét hình thang BCC'B' có
M,M' lần lượt là trung điểm của CB,C'B'
=>MM' là đường trung bình
=>MM'//BB'//CC'
=>MM'//AA'
Xét tứ giác AA'M'M có
MM'//AA'
AM=A'M'
Do đó: AA'M'M là hình bình hành
=>AM//A'M'
=>AG//A'G'
=>A'G'//(ABCD)

Đáp án C
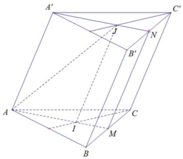
Xét tam giác A’B’C’:
Gọi N là trung điểm B’C’
J là trọng tâm A’B’C’
![]()
Xét tam giác ABC:
Gọi M là trung điểm BC
I là trọng tâm ABC
![]()
Từ (1), (2), ta có IJ // MN
Xét (AIJ) và (B’C’CB) có:
M là điểm chung
IJ // MN
⇒ giao tuyến của (AIJ) và (B’C’CB) là MN
⇒ thiết diện cần tìm là mặt phẳng (A’NMA)
Xét (A’NMA) có: A’A // MN và A’A = MN ( // = BB’)
A’NMA là hình hình hành

Đáp án D
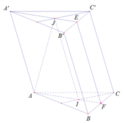
Gọi E và F lần lượt là trung điểm của B’C’ và BC
Xét (AIJ) và (ABC) có: F ∈ AI ⇒ F ∈ (AIJ) ⇒ (AIJ) ∩ (ABC) = AF
Xét ( AIJ) và (B’C’CB) có : F là điểm chung
IJ // (B’C’CB) ( I; J lần lượt là trọng tâm tam giác ABC và A’B’C’)
⇒ giao tuyến của 2 mặt phẳng là đường thẳng a đi qua F và song song IJ
a cắt B’C’ tại E
⇒ (AIJ) ∩ (B’C’CB) = EF
Xét ( AIJ) và (A’B’C’) có:
E là điểm chung
AF // (A’B’C’)
⇒ giao tuyến 2 mặt phẳng là đường thẳng b đi qua E và song song AF
⇒ (AIJ) ∩ (A’B’C’) = A’E
Xét A’EFA có: AA’ // EF ( // IJ)
A’E // AF
A’EFA là hình bình hành


Hướng dẫn:
Dễ dàng nhận ra A thuộc B'G (vì AB' là đường chéo của hbh mặt bên nên là 1 trung tuyến)
Gọi M, M' lần lượt là trung điểm BC và B'C'
=> (GOB') là (AMB')
(CA'O') là (CA'M')
Có B'M'CM là hình bình hành
A'M'MA cũng là hbh
Suy ra 2 cặp đường thẳng song song và cắt nhau => đpcm