Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hướng dẫn:
Gọi P, H lần lượt là trung điểm CD, B'C' \(\Rightarrow\) PMHN là hình chữ nhật
Gọi K, G lần lượt là giao điểm của AC và PM, A'C' là HN \(\Rightarrow\) K, G lần lượt là trung điểm PM và NH
Điểm E chính là giao điểm của MN và KG.
Với việc K, G là trung điểm 2 cạnh đối hcn và MN là đường chéo của hcn thì hiển nhiên E sẽ là trung điểm MN
b.
Do E là trung điểm PG (và MN) nên QE song song AC
Do đó QE, AC', BD' cùng đi qua tâm I của lập phương
c.
Như câu b thì I đồng thời là tâm lập phương
QI đi qua trung điểm E của MN đồng thời \(\frac{QI}{QE}=\frac{AO}{AK}=\frac{2}{3}\) (với O là tâm hình vuông ABCD) nên I là trọng tâm QMN

Hướng dẫn:
Dễ dàng nhận ra A thuộc B'G (vì AB' là đường chéo của hbh mặt bên nên là 1 trung tuyến)
Gọi M, M' lần lượt là trung điểm BC và B'C'
=> (GOB') là (AMB')
(CA'O') là (CA'M')
Có B'M'CM là hình bình hành
A'M'MA cũng là hbh
Suy ra 2 cặp đường thẳng song song và cắt nhau => đpcm

Do \(\left\{{}\begin{matrix}AA'\perp\left(ABCD\right)\Rightarrow AA'\perp AD\\AD\perp AC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow AD\perp\left(AA'C\right)\)
Mà \(AD||A'D'\Rightarrow A'D'\perp\left(AA'C\right)\)
Lại có \(AA'||CC'\Rightarrow C'\in\left(AA'C\right)\Rightarrow A'D'\perp AC'\) (1)
\(\left\{{}\begin{matrix}AA'\perp AC\\AA'=AC\end{matrix}\right.\) \(\Rightarrow\) tứ giác AA'C'C là hình vuông
\(\Rightarrow AC'\perp A'C\) (2)
(1);(2) \(\Rightarrow AC'\perp\left(A'D'C\right)\)

\(AH\perp\left(ABCD\right)\Rightarrow\widehat{A'AH}\) là góc giữa AA' và (ABCD) \(\Rightarrow\widehat{A'AH}=60^0\)
\(\Rightarrow AA'=\dfrac{AH}{cos60^0}=a\)
a. Ta có: \(\left\{{}\begin{matrix}A'H\perp\left(ABCD\right)\Rightarrow A'H\perp AD\\AD\perp AB\end{matrix}\right.\) \(\Rightarrow AD\perp\left(ABB'A'\right)\)
Mà \(AD\in\left(ADD'A'\right)\Rightarrow\left(ADD'A'\right)\perp\left(ABB'A'\right)\)
b. Kiểm tra lại đề câu này
Hai mặt phẳng (ABCD) và (A'B'C'D') hiển nhiên song song (theo tính chất lăng trụ) nên góc giữa chúng bằng 0. Do đó thấy ngay \(tan\left(\left(ABCD\right);\left(A'B'C'D'\right)\right)=0\)
Có lẽ không ai bắt tính điều này cả.
c.
\(\left(ABCD\right)||\left(A'B'C'D'\right)\Rightarrow d\left(A;\left(A'B'C'D'\right)\right)=d\left(A';\left(ABCD\right)\right)=A'H=a\)
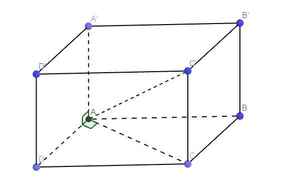
a: ABCD.A'B'C'D là hình hộp chữ nhật
=>AA'//DD'//BB'//CC'
AA'//CC'
=>AA'//(CC'D'D)
B'B//D'D
=>B'B//(CC'D'D)
mà AA'//(CC'D'D)
và A'A và B'B cùng thuộc mp(AA'B'B)
nên (AA'B'B)//(CC'D'D)
b: Xét tứ giác ADC'B' có
AD//B'C'
AD=B'C'
Do đó: ADC'B' là hình bình hành
=>AB'//DC'
=>AB'//(C'BD)(1)
Xét tứ giác BDD'B' có
BB'//DD'
BB'=D'D
Do đó: BDD'B' là hình bình hành
=>BD//B'D'
=>B'D'//(C'BD)(2)
Từ (1) và (2) suy ra (C'BD)//(AB'D')
c: Gọi G là trọng tâm của ΔABC
Xét ΔBAC có
BO là đường trung tuyến
G là trọng tâm
Do đó: B,O,G thẳng hàng và \(BG=\dfrac{2}{3}BO\)
Gọi M là giao điểm của AG với BC; M' là giao điểm của A'G' với B'C'
Xét ΔABC có
G là trọng tâm
M là giao điểm của AG với BC
Do đó: M là trung điểm của BC và \(AG=\dfrac{2}{3}AM\)
Xét ΔA'B'C' có
G' là trọng tâm
A'G' cắt B'C' tại M'
Do đó: M' là trung điểm của B'C'
Xét ΔABM và ΔA'B'M' có
AB=A'B'
\(\widehat{ABM}=\widehat{A'B'M'}\)
BM=B'M'
Do đó: ΔABM=ΔA'B'M'
=>AM=A'M'
Xét hình thang BCC'B' có
M,M' lần lượt là trung điểm của CB,C'B'
=>MM' là đường trung bình
=>MM'//BB'//CC'
=>MM'//AA'
Xét tứ giác AA'M'M có
MM'//AA'
AM=A'M'
Do đó: AA'M'M là hình bình hành
=>AM//A'M'
=>AG//A'G'
=>A'G'//(ABCD)