Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) dựa vào tính chất đường phân giác" BM/BD=AM/AD" và "MC/EC=AM/AE"
bạn rút 2 vế ra được..."BM/AM=BD/AD=EC/AE" ( mà MC=BM)
dựa theo tính chất talet đảo => DE//BC
tk nha bạn
thank you bạn
(^_^)

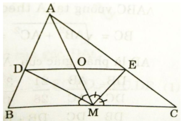
a) DM là đường phân giác của ΔABM nên theo tính chất đường phân giác của tam giác ta có:
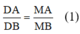
Tương tự EM là đường phân giác ΔACM nên:
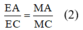
Mà MB = MC nên từ (1) và (2) suy ra

![]()
![]()
![]()
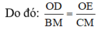
![]()

a: Xét ΔMAB có MD là phan giác
nên MA/MB=AD/DB=MA/MC
Xét ΔMAC có ME là phân giác
nên MA/MC=AE/EC
=>AD/DB=AE/EC
=>DE//BC
b: Xét ΔAMB có OD//MB
nên OD/MB=AO/AM
Xét ΔAMC có OE//MC
nên OE/MC=AO/AM
=>OD/MB=OE/MC
mà MB=MC
nên OD=OE

a, Vì MD là phân giác AMB \(\Rightarrow\frac{AD}{AM}=\frac{BD}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)\(\Rightarrow\frac{AD}{BD}=\frac{AM}{CM}\)(MB = MC)
Vì ME là phân giác AMC \(\Rightarrow\frac{AE}{AM}=\frac{EC}{MC}\)\(\Rightarrow\frac{AE}{EC}=\frac{AM}{MC}\)
\(\Rightarrow\frac{AE}{EC}=\frac{AD}{BD}\) => DE // BC (định lý Thales đảo)
b, Vì DE // BE (cmt) \(\Rightarrow\frac{DO}{BM}=\frac{AO}{OM}\)(Hệ quả định lý Thales) và \(\frac{OE}{MC}=\frac{OA}{OM}\) (Hệ quả định lý Thales)
\(\Rightarrow\frac{DO}{BM}=\frac{OE}{MC}\)
Mà BM = MC (gt)
=> DO = OE

a) Vì AM là trung tuyến của \(\Delta ABC\Rightarrow BM=CM;M\in BC\)
Xét \(\Delta ABM\)có MD là p/g \(\widehat{BMA}\Rightarrow\frac{AD}{BD}=\frac{AM}{BM}\)hay \(\frac{AD}{BD}=\frac{AM}{CM}\left(1\right)\)
Xét \(\Delta ACM\)có ME là p/g \(\widehat{CMA}\Rightarrow\frac{AE}{CE}=\frac{AM}{CM}\left(2\right)\)
Từ (1)(2)\(\Rightarrow\frac{AD}{BD}=\frac{AE}{CE}\Rightarrow DE//BC\)(đ/ lí Ta-lét đảo)
b) Có \(DE//BC\), \(O\in DE,M\in BC\Rightarrow OD//BM;OE//CM\)
Xét \(\Delta ABM\)có \(OD//BM\Rightarrow\frac{OD}{BM}=\frac{OA}{AM}\left(3\right)\)
Xét \(\Delta ACM\)có \(OE//CM\Rightarrow\frac{OE}{CM}=\frac{OA}{AM}\left(4\right)\)
Từ (3)(4) \(\Rightarrow\frac{OD}{BM}=\frac{OE}{CM}\).Mà BM=CM \(\Rightarrow OD=OE\)

a) 
b) ta có MD là tia phân giác của \(\widehat{AMB}\), ME là tia phân giác của \(\widehat{AMC}\)
=> \(\widehat{AMD}=\widehat{DMB}=\dfrac{1}{2}\widehat{AMB}\) và \(\widehat{AME}=\widehat{EMC}=\dfrac{1}{2}\widehat{AMC}\)
=> \(\widehat{AME}+\widehat{AMD}=\dfrac{\widehat{AMC}+\widehat{AMB}}{2}=\dfrac{180^o}{2}=90^o\)
Ta có \(\widehat{EMC}=\widehat{MED}\)(do ED//BC)
mà \(\widehat{EMC}=\widehat{EMI}\)
=> \(\widehat{EMI}=\widehat{MEI}\)=> tam giác EIM cân tại I
=> EI=IM
cmtt : IM=ID
=> EI=IM=MD
=> IM = \(\dfrac{1}{2}\left(EI+ID\right)=\dfrac{1}{2}ED\)(ĐPCM)

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD

Câu 3:
Xét ΔMDC có AB//CD
nên MA/MD=MB/MC(1)
Xét ΔMDK có AI//DK
nên AI/DK=MA/MD(2)
Xét ΔMKC có IB//KC
nên IB/KC=MB/MC(3)
Từ (1), (2) và (3) suy ra AI/DK=IB/KC=MI/MK
Vì AI//KC nên AI/KC=NI/NK=NA/NC
Vì IB//DK nên IB/DK=NI/NK
=>AI/KC=IB/DK
mà AI/DK=IB/KC
nên \(\dfrac{AI}{KC}\cdot\dfrac{AI}{DK}=\dfrac{IB}{DK}\cdot\dfrac{IB}{DC}\)
=>AI=IB
=>I là trung điểm của AB
AI/DK=BI/KC
mà AI=BI
nên DK=KC
hay K là trung điểm của CD