Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

tham khảo
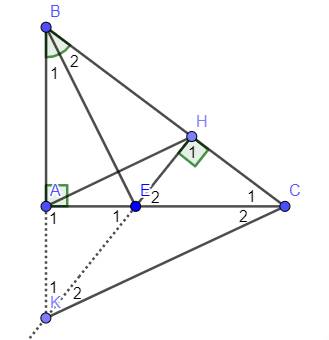
a) Xét tam giác vuông ABE và tam giác vuông HBE (^BAE = ^BHE = 90o)
BE chung
^ABE = ^HBE (BE là phân giác ^ABC)
=> tam giác vuông ABE = tam giác vuông HBE (ch - gn)
b) Ta có: AE = HE (tam giác vuông ABE = tam giác vuông HBE)
=> E thuộc đường trung trực của AH (1)
Ta có: AB = HB (tam giác vuông ABE = tam giác vuông HBE)
=> B thuộc đường trung trực của AH (2)
Từ (1) và (2) => BE là đường trung trực của AH (đpcm)
c) Ta có: ^BEK = ^BEA + ^AEK
^BEC = ^BEH + ^HEC
Mà ^BEA = ^BEH (tam giác vuông ABE = tam giác vuông HBE)
^AEK = ^HEC (2 góc đối đỉnh)
=> ^BEK = ^BEC
Xét tam giác BEK và tam giác BEC:
^BEK = ^BEC (cmt)
^KBE = ^CBE (BE là phân giác ^ABC)
BE chung
=> tam giác BEK = tam giác BEC (g - c - g)
=> EK = EC (cặp cạnh tương ứng)

a: Xét ΔBKC có
KH,CA là đường cao
KH cắt CA tại E
=>E là trực tâm
=>BE vuông góc KC
b: Xét ΔBAE vuông tại A và ΔBHE vuông tại H có
BE chung
góc ABE=góc HBE
=>ΔBAE=ΔBHE
=>BA=BH
c: Xét ΔBKC có
BE vừa là đường cao, vừa là phân giác
=>ΔBKC cân tại B

C1 :
Hình : tự vẽ
a )Vì CA=CB ( đề bài cho ) => tam giác ABC cân tại C
mà CI vuông góc vs AB => CI là đường cao của tam giác ABC
=> CI cũng là đường trung tuyến của tam giác ABC ( t/c tam giác cân )
=> IA=IB (đpcm)
C1 :
b) Có IA=IB ( cm phần a )
mà IA+IB = AB
IA + IA = 12 (cm)
=> IA = \(\frac{12}{2}=6\left(cm\right)\)
Xét tam giác vuông CIA có : CI2 + IA2 = CA2 ( Đ/l Py-ta -go )
CI2 + 62 = 102
CI2 = 102 - 62 = 64
=> CI = \(\sqrt{64}=8\left(cm\right)\)
Vậy CI ( hay IC ) = 8cm

1. ΔABE = ΔHBE
Xét ΔABE và ΔHBE, ta có :
(gt)
( BE là đường phân giác của góc HBA).
BE là cạnh chung.
=> ΔABE = ΔHBE
2. BE là đường trung trực của AH :
BA =BH và EA = EH (ΔABE = ΔHBE)
=> BE là đường trung trực của AH .
3. EK = EC
Xét ΔKAE và ΔCHE, ta có :
(gt)
EA = EH (cmt)
( đối đỉnh).
=> ΔKAE và ΔCHE
=> EK = EC
4. EC > AC
Xét ΔKAE vuông tại A, ta có :
KE > AE (KE là cạnh huyền)
Mà : EK = EC (cmt)
=> EC > AC.

Xét ΔABE và ΔHBE có:
\(\widehat{BAE}=\widehat{BHE}=90\) (gt)
BE:cạnh chung
\(\widehat{ABE}=\widehat{HBE}\left(gt\right)\)
=> ΔABE =ΔHBE(cạnh huyền-góc nhọn)
b) Vì ΔABE=ΔHBE(cmt)
=> AB=BH ; AE=EH
=> B,E \(\in\) đường trung trực của đoạn thẳng AH
=>BE là đường trung trực của đoạn thẳng AH
c) Xét ΔAEK và ΔHEC có:
\(\widehat{KAE}=\widehat{CHE}=90\left(gt\right)\)
AE=EH(cmt)
\(\widehat{AEK}=\widehat{HEC}\)
=>ΔAEK=ΔHEC(g.c.g)
=>EK=EC
d) Xét ΔEHC vuông tại H(gt)
=> HE<EC
Mà: HE=AE(cmt)
=>AE<EC
d) Xét ΔHKC có:
KH,CA là hai đường cao
=> E là trực tâm của ΔBKC
=>BE là đường cao
=> AE vuông góc KC
a)
xét 2 tam giác vuông ABE và HBE có:
BE(chung)
góc ABE= góc CBE(gt)
=> ΔABE=ΔHBE(CH-GN)
b)
gọi giao của BE và AH là F
xét ΔABF và ΔHBF có:
AB=HB(theo câu a, ΔABE=ΔHBE)
BF(chung)
góc ABE=góc HBE(gt)
=> ΔABF=ΔHBF(c.g.c)
=>\(\begin{cases}FA=FH\\\widehat{AFB}=\widehat{BFH}=180^o:2=90^o\end{cases}\)
=> BE là đường trung trực của AH
c)
xét ΔAEK và ΔHEC có:
EA=EH(theo câu a, ΔABE=ΔHBE)
góc KAE=góc EHC=90º(gt)
góc AEK=góc CEH(2 góc đối đỉnh)
=>ΔAEK=ΔHEC(g.c.g)
=>EK=EC
d)
ta có ΔAEK vuông tại A
=> EK>AE
mà EK=EC(theo câu c)
=> AE<EC
e)
theo câu a, ta có: ΔABE=ΔHBE(CH-GN)
=>AB=HB
theo câu c, ta có: ΔAEK=ΔHEC(g.c.g)
=> AK=HC
ta có: KB=KA+AB
CB=CH+HB
=>KB=CB
=>ΔKBC cân tại B
ta có:ΔKCB cân tại B có BE là đường phân giác
=>BE đồng thời là đường cao của ΔKBC
=>BE_|_KC
f)
áp dụng định lí py-ta-go ta có;
\(AC^2=BC^2-AB^2=5^2-3^2=25-9=16\)
\(AC=\sqrt{16}=4\left(cm\right)\)
theo câu e; ta có ΔKBC cân tại B
=> BC=BK=5cm
AK=BC-AB=5cm-3cm=2cm
áp dụng định lí py-ta-go ta có:
\(KC^2=AK^2+AC^2=4^2+2^2=16+4=20\)
\(KC=\sqrt{20}\left(cm\right)\)