Question

[Nguyễn Thu Mùi]

Cho tam giác ABC vuông tại A,đường phân giác của góc BAC cắt BC tại D.Từ D kẻ DE vuông góc AB tại E.

a.c/m AC.BE=AB.EA

b.Qua A kẻ đường thẳng song song với BC cắt DE tại F,qua D kẻ đường thẳng song song với AB cắt AC tại I,cắt FA tại K.c/m FA/FK + KI/KD=1

Answer 1

[Vũ Đào Duy Hùng (haeng2010)]

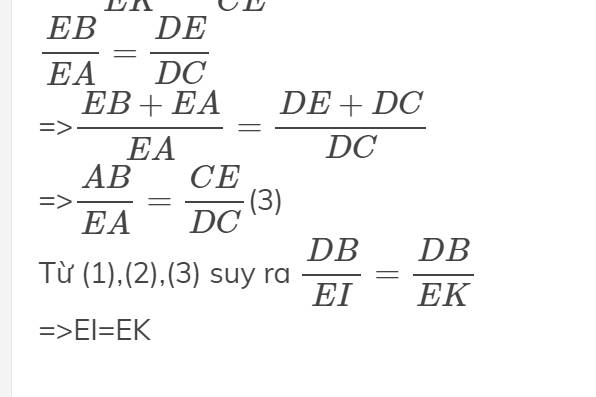
a. Theo định lý về đường phân giác trong tam giác, ta có:
$\frac{AB}{AC} = \frac{BD}{DC} \tag{1}$
Vì DE vuông góc với AB tại E, nên theo định lý Pythagoras, ta có:
$AE^2 = AB^2 - BE^2 \tag{2}$
$DE^2 = DB^2 - BE^2 \tag{3}$
Từ (2) và (3), ta có:
$AE^2 = DE^2 \Rightarrow AE = DE \tag{4}$
Từ (1) và (4), ta có:
$\frac{AB}{AC} = \frac{DE}{DC} = \frac{AE}{DC} \Rightarrow AC.BE = AB.EA$
b. Do AF // BC và AD cắt BC tại D, AF cắt AD tại K nên ta có:
$\frac{FA}{FK} = \frac{DA}{DK} \tag{5}$
Do DI // AB và DC cắt AB tại B, DI cắt DC tại K nên ta có:
$\frac{KI}{KD} = \frac{BI}{BD} \tag{6}$
Từ (5) và (6), ta có:
$\frac{FA}{FK} + \frac{KI}{KD} = \frac{DA}{DK} + \frac{BI}{BD} = 1$

Answer 2

[Vũ Đào Duy Hùng (haeng2010)]

Bạn ơi mình xin lỗi nhé, bài mình bị lỗi latex T-T