Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


∆ABC có M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm N sao cho MN = MA.
Ta có:
ےAMB = ےNMC (đối đỉnh)
BM = CM (giả thiết)
MA = MN (dựng hình)
Suy ra: ∆MAB = ∆MNC (c.g.c)
Suy ra: NC = AB và ےMBA = ےMCN
Do ےMBA = ےMCN nên AB // NC
Suy ra ےBAC + ےACN = 180
Ta có: ےBAC = 90 nên ےACN = 90
=> ∆ABC = ∆CNA (c.g.c) vì AC là cạnh chung
AB = NC (cmt) và ےBAC = ےACN = 90
=> AN = BC
=> AM = \(\frac{1}{2}BC\)
=>CMT

vẽ thêm MD song song AH
MH song song AD
Xét tam giác MDA và tam giác AHM có
Góc A1 = góc M2 (so le trong)
Góc A2 = góc M1 ( so le trong)
AM là cạnh chung
\(\Rightarrow\)Tam giác MDA = tam giác AHM (g.c.g)
\(\Rightarrow\)MD = AH (2 cạnh tương ứng)
Xét tam giác MBD và tam giác CMH có
Góc BMD = góc MCH (đồng vị)
Góc D1 = góc H2 (=90)
BM = MC (giả thiết)
\(\Rightarrow\)Tam giác MBD = tam giác CMH (cạnh huyền - góc nhọn)
\(\Rightarrow\)BD = MH ( 2 cạnh tương ứng)
Xét tam giác BDM và tam giác MHA có
MD = AH ( cmt)
Góc D2 = góc H1 (=90)
BD = MH (cmt)
\(\Rightarrow\)tam giác MBD = tam giác MAH ( c.g.c)
\(\Rightarrow\)BM = AM (2 cạnh tương ứng)
Vì BM = MC và AM = BM
\(\Rightarrow\)AM = MC
Mà BC = BM + MC
\(\Rightarrow\)BC = 2*AM
\(\Rightarrow\)AM = \(\frac{1}{2}\cdot BC\)
Vậy AM = \(\frac{1}{2}\cdot BC\)

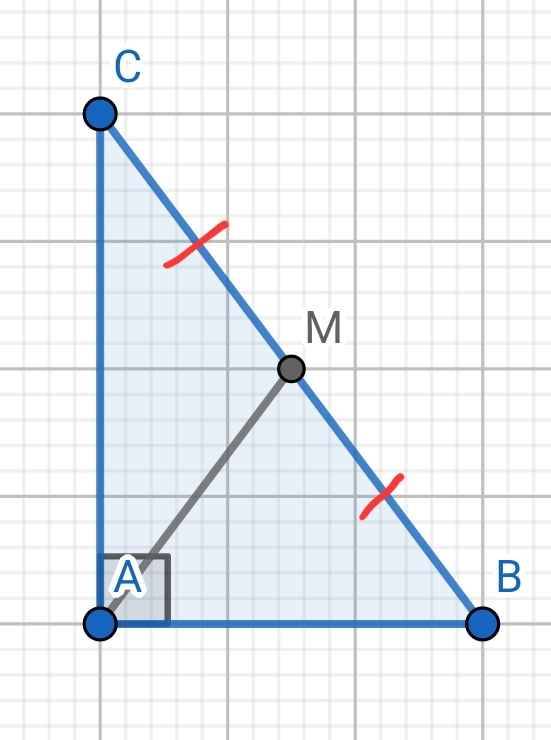
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2

a: Xét ΔBAC có
MN//AB
nên CMCB=MNABCMCB=MNAB
⇔MN=6⋅12=3(cm)⇔MN=6⋅12=3(cm)
b: Vì M đối xứng với E qua AC
nên AC là đường trung trực của ME
mà AC cắt ME tại N
nên N là trung điểm của ME
Xét tứ giác AMCE có
N là trung điểm của đường chéo ME
N là trung điểm của đường chéo AC
Do đó: AMCE là hình bình hành
b: Xét tứ giác ABDC có
AB//DC
AB=DC
DO đó: ABDC là hình bình hành
mà \(\widehat{BAC}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: AD=BC

a)

Xét 2 tam giác vuông AMC và AMB có:
AM chung
BM=CM (gt)
=>\(\Delta AMC = \Delta AMB\) (hai cạnh góc vuông)
=> AC=AB (2 cạnh tương ứng)
=> Tam giác ABC cân tại A
b)

Kẻ MH vuông góc với AB (H thuộc AB)
MG vuông góc với AC (G thuộc AC)
Xét 2 tam giác vuông AHM và AGM có:
AM chung
\(\widehat {HAM} = \widehat {GAM}\) (do AM là tia phân giác của góc BAC)
=>\(\Delta AHM = \Delta AGM\) (cạnh huyền – góc nhọn)
=> HM=GM (2 cạnh tương ứng)
Xét 2 tam giác vuông BHM và CGM có:
BM=CM (giả thiết)
MH=MG(chứng minh trên)
=>\(\Delta BHM = \Delta CGM\)(cạnh huyền – cạnh góc vuông)
=>\(\widehat {HBM} = \widehat {GCM}\)(2 góc tương ứng)
=>Tam giác ABC cân tại A.

Trên tia đối của tia MA, lấy điểm D sao cho MA=MD
Xét tứ giác ACDB có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ACDB là hình bình hành
Hình bình hành ACDB có \(\widehat{CAB}=90^0\)
nên ACDB là hình chữ nhật
Suy ra: BC=AD
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)


Lời giải:
a.
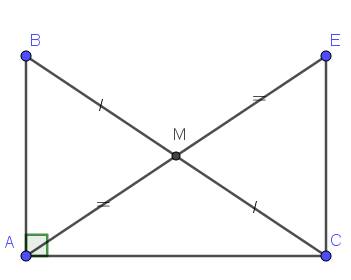
Xét tam giác $AMB$ và $EMC$ có:
$\widehat{AMB}=\widehat{EMC}$ (đối đỉnh)
$AM=EM$
$MB=MC$
$\Rightarrow \triangle AMB=\triangle EMC$ (c.g.c)
b.
Vì $\triangle AMB=\triangle EMC$ nên $\widehat{MAB}=\widehat{MEC}$
Mà 2 góc này ở vị trí so le trong nên $EC\parallel AB$
Mà $AB\perp AC$ nên $EC\perp AC$ (đpcm)
c.
Vì $\triangle AMB=\triangle EMC$ nên:
$AB=EC$
Vì $EC\perp AC$ nên $\widehat{ECA}=90^0=\widehat{BAC}$
Xét tam giác $ECA$ và $BAC$ có:
$\widehat{ECA}=\widehat{BAC}=90^0$ (cmt)
$AC$ chung
$EC=BA$ (cmt)
$\Rightarrow \triangle ECA=\triangle BAC$ (c.g.c)
$\Rightarrow EA=BC$
Mà $EA=2AM$ nên $2AM=BC$ (đpcm)