Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Áp dụng định lí Pi-ta-go vào tam giác vuông BDM, ta có:
B M 2 = B D 2 + D M 2 ⇒ B D 2 = B M 2 - D M 2 (1)
Áp dụng định lí Pi-ta-go vào tam giác vuông CEM, ta có:
C M 2 = C E 2 + E N 2 ⇒ C E 2 = C M 2 - E M 2 (2)
Áp dụng định lí Pi-ta-go vào tam giác vuông AFM, ta có:
A M 2 = A F 2 + F M 2 ⇒ A F 2 = A M 2 - F M 2 (3)
Cộng từng vế của (1), (2) và (3) ta có:
B D 2 + C E 2 + A F 2 = B M 2 - D M 2 + C M 2 - E M 2 + A M 2 - F M 2 (4)
Áp dụng định lí Pi-ta-go vào tam giác vuông BFM, ta có:
B M 2 = B F 2 + F M 2 (5)
Áp dụng định lí Pi-ta-go vào tam giác vuông CDM, ta có:
C M 2 = C D 2 + D M 2 (6)
Áp dụng định lí Pi-ta-go vào tam giác vuông AEM, ta có:
A M 2 = A E 2 + E M 2 (7)
Thay (5), (6), (7) vào (4) ta có:
B D 2 + C E 2 + A F 2 = B F 2 + F M 2 - D M 2 + C D 2 + D M 2 - E M 2 + A E 2 + E M 2 - F M 2 = D C 2 + E A 2 + F B 2
Vậy B D 2 + C E 2 + A F 2 = D C 2 + E A 2 + F B 2

Bạn ơi đề thiếu hay sao ấy
Phải là :
BD2 - CD2 = ?
Sửa đi mik giải cho

Cho tam giác ABC vuông tại A, M là trung điểm của AC. Vẽ MD vuông góc với BC ( D thuộc BC ) . Chứng minh : AB2 = BD2 - CD2 .

a ) Ta có : \(\widehat{A}=\widehat{D}=\widehat{E}=90^o\left(gt\right)\)
\(\Rightarrow ADME\) là hình chữ nhật ( tứ giác có ba góc vuông )
b ) Ta có : ME là đường trung bình của tam giác ABC
\(\Rightarrow ME//AB\) và \(ME=\frac{1}{2}AB=\frac{1}{2}.6=3\left(cm\right)\)
\(\Rightarrow AD=ME=3\left(cm\right)\)( cạnh đối hình chữ nhật )
Lại có : \(\hept{\begin{cases}ME//AB\left(cmt\right)\\MB=MC\left(gt\right)\end{cases}}\)
\(\Rightarrow AE=CE=\frac{AC}{2}=\frac{8}{2}=4\left(cm\right)\)
ADME : hình chữ nhật
\(\Rightarrow A_{ADME}=AD.AE=3.4=12\left(cm^2\right)\)
c ) Dễ thấy AC là đường trung trực của MK
\(\Rightarrow AM=AK\)và \(CM=CK\)
Mà AM = CM \(\left(=\frac{1}{2}BC\right)\) ( \(\Delta ABC\) vuông tại A )
\(\Rightarrow AM=AK=CM=CK\)
\(\Rightarrow AMCK\)là hình thoi ( tứ giác có 4 cạnh bằng nhau )
d ) Ta có : \(ME=\frac{1}{2}AB\)
\(\Rightarrow AB=2ME=MK\)
Hình thoi AMCK là hình vuông \(\Leftrightarrow AC=MK\)
\(\Leftrightarrow AC=AB\) ( vì AB = MK )
\(\Leftrightarrow\Delta ABC\)cân tại A
Mà \(\Delta ABC\) vuông tại A (gt)
Vậy \(\Delta ABC\)vuông cân tại A thì hình thoi AMCK là hình vuông

2: Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
mà \(\widehat{CAB}=90^0\)
nên ABDC là hình chữ nhật
Suy ra: CD=AB(1)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(AB^2=BH\cdot BC\left(2\right)\)
Từ (1) và (2) suy ra \(CD^2=BH\cdot BC\)

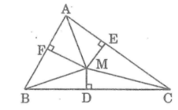
a) Ta có: Đường tròn (O) đường kính BC và 2 điểm D;E nằm trên (O)
=> ^BEC=^BDC=900 => BD vuông AC; CE vuông AB
Mà BD gặp CE tại H => H là trực tâm \(\Delta\)ABC
=> AH vuông BC (tại F) hay AF vuông BC (đpcm).
b) Thấy: \(\Delta\)ADH vuông đỉnh D, M là trg điểm AH
=> \(\Delta\)DMA cân đỉnh M => ^MDA=^MAD (1).
Tương tự: \(\Delta\)DOC cân đỉnh O => ^ODC=^OCD (2).
(1) + (2) => ^MAD+^ODC = ^MDA+^ODC = ^MAD+^OCD
Mà 2 góc ^MAD; ^OCD phụ nhau (Do \(\Delta\)AFC vuông đỉnh F)
=> ^MDA+^ODC=900 => ^MDO=900 => MD vuông OD
Lập luận tương tự: ME vuông OE => Tứ giác MEOD có ^MEO=^MDO=900
=> MEOD là tứ giác nội tiếp đường tròn đường kính OM
Xét tứ giác MFOD: ^MFO=^MDO=900 => Tứ giác MFOD nội tiếp đường tròn đường kính MO.
Do đó: 5 điểm M;D;O;E;F cùng thuộc 1 đường tròn đường kính OM (đpcm).
c) Dễ c/m \(\Delta\)EBF ~ \(\Delta\)CDF (c.g.c) => ^EFB=^CFD
=> 900 - ^EFB = 900 - ^CFD => ^EFA=^DFA hay ^EFM=^MFD
Xét tứ giác FEMD: Nội tiếp đường tròn => ^EFM=^KDM => ^MFD=^KDM
=> \(\Delta\)MKD ~ \(\Delta\)MDF (g.g) => \(\frac{MD}{MF}=\frac{MK}{MD}\Rightarrow MD^2=MK.MF\)(đpcm).
Gọi I là giao điểm BK và MC.
Dễ thấy: \(\Delta\)FEK ~ FMD (g.g) => \(\frac{FE}{FM}=\frac{FK}{FD}\Rightarrow FE.FD=FM.FK\)
Hoàn toàn c/m được: \(\Delta\)EFB ~ \(\Delta\)CFD (c.g.c) => \(\frac{FE}{FC}=\frac{BF}{FD}\Rightarrow FE.FD=BF.FC\)
Từ đó suy ra: \(FM.FK=BF.FC\)\(\Rightarrow\frac{BF}{FM}=\frac{FK}{FC}\)
\(\Rightarrow\Delta\)BFK ~ \(\Delta\)MFC (c.g.c) => ^FBK=^FMC . Mà ^FMC+^FCM=900
=> ^FBK+^FCM = 900 hay ^FBI+^FCI=900 => \(\Delta\)BIC vuông đỉnh I
=> BK vuông với MC tại điểm I.
Xét \(\Delta\)MBC: BK vuông MC (cmt); MK vuông BC (tại F) => K là trực tâm \(\Delta\)MBC (đpcm).
d) Thấy ngay: EH là phân giác trong của \(\Delta\)FEK. Mà EA vuông EH
=> EA là phân giác ngoài tại đỉnh E của \(\Delta\)FEK
Theo ĐL đường phân giác trg tam giác: \(\frac{KH}{FH}=\frac{AK}{AF}\)
\(\Leftrightarrow1+\frac{KH}{FH}=1+\frac{AK}{AF}\Rightarrow\frac{FK}{FH}=\frac{AK+AF}{AF}\Leftrightarrow\frac{FK}{FH}=\frac{FK+2AK}{AF}\)
\(\Leftrightarrow\frac{FK}{FH}=\frac{FK}{AF}+\frac{2AK}{AF}\Leftrightarrow\frac{FK}{AF}=\frac{FK}{FH}-\frac{2AK}{AF}\)
\(\Leftrightarrow\frac{FK}{AF}+\frac{FK}{FH}=\frac{2FK}{FH}-\frac{2AK}{AF}=2+\frac{2KH}{FH}-2+\frac{2KF}{AF}=\frac{2KH}{FH}+\frac{2KF}{AF}\)
\(\Rightarrow FK\left(\frac{1}{AF}+\frac{1}{FH}\right)=\frac{2KH}{FH}+\frac{2KF}{AF}\)
Đến đây, lại thay: \(\frac{KH}{FH}=\frac{AK}{AF}\)(T/c đg phân giác)
\(\Rightarrow FK\left(\frac{1}{AF}+\frac{1}{FH}\right)=\frac{2\left(AK+KF\right)}{AF}=\frac{2AF}{AF}=2\)
\(\Leftrightarrow\frac{1}{AF}+\frac{1}{FH}=\frac{2}{FK}.\)(đpcm).
d.
Xét△FBH và △FAC có BFH=AFC=90*,FBH=FAC(cùng phụ BCD)
=>△FBH∼ △FAC(g.g) =>FH.FA=FB.FC .
Xét△FBK và △FMC có BFK=MFC=90*, FBK=FMC
=>△FBK ∼ △FMC(g.g)=>FK.FM=FB.FC .
=>FH.FA=FK.FM
Mà FH+FA=FM-MH+FM+MA=2FM
Ta có 2FH.FA=2FK.FM=>2FH.FA=FK(FH+FA)=>KL