Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔABC vuông tại A và ΔHBA vuông tại H có
\(\widehat{ABC}\) chung
Do đó: ΔABC∼ΔHBA(g-g)

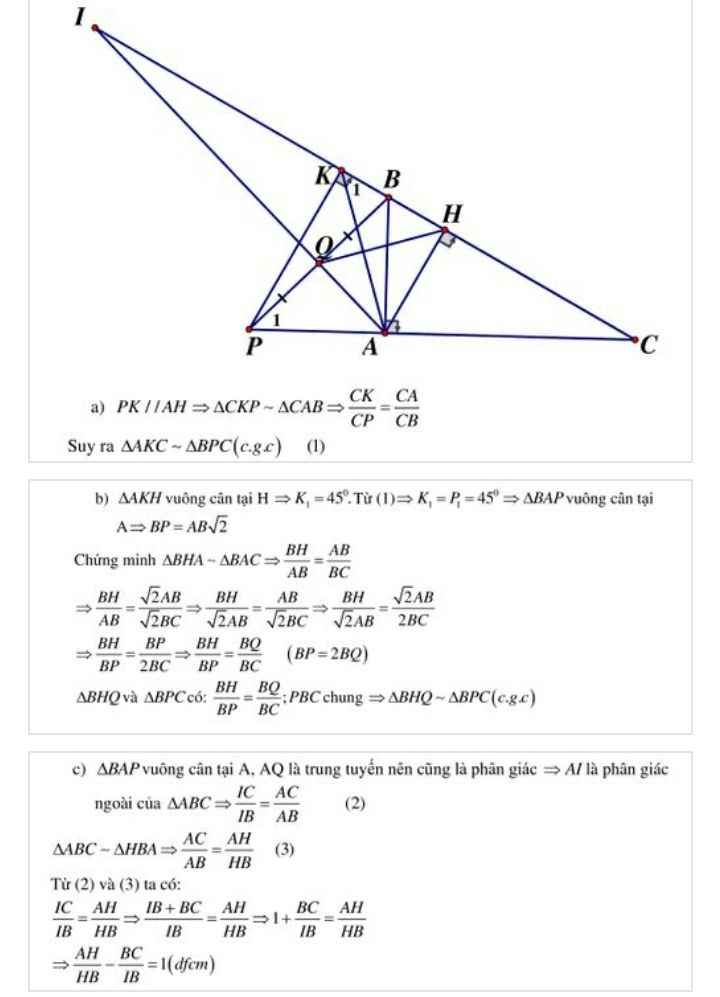
a) Ta có AI = AK ; AB = AC => AI / AB = AK/ AC => IK // BC (Định lí Ta lét)
Tam giác ABC cân tại A có AH là đường cao => AH I BC
=> AH I IK
Mặt khác, tam giác AIK cân tại A : AH là đường cao nên đồng thời là đường trung trực
=> I và K đối xứng qua AH

Đọc đề là sai r bn ạ . Ban đầu ko cho I mà lại bạo phải c/m tam giác AKI nhỏ hơn hoặc 1/2 tam giác ABC.
XEM LẠI ĐỀ NHA

a) Xét \(\Delta ABC\) và \(\Delta HAC\) có:
\(\widehat{BAC}=\widehat{AHC}=90^0\)
\(\widehat{ABC}=\widehat{HAC}\) do cùng phụ với góc BAH )
suy ra: \(\Delta ABC~\Delta HAC\)
b) Áp dụng định lý Pytago ta có:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow\)\(BC^2=6^2+8^2=100\)
\(\Leftrightarrow\)\(BC=\sqrt{100}=10\)
Áp dụng hệ thức lượng ta có:
\(AH=\frac{AB.AC}{BC}=\frac{6.8}{10}=4,8\)cm
\(CH=\frac{AC^2}{BC}=\frac{8^2}{10}=6,4\)cm
\(BH=BC-HC=10-6,4=3,6\)cm

a: Xét ΔHBA vuông tại H và ΔABC vuông tại A có
góc HBA chung
Do đó:ΔHBA\(\sim\)ΔABC
b: ta có: ΔHBA\(\sim\)ΔABC
nên BH/BA=BA/BC
hay \(BA^2=BH\cdot BC\)

a: Xét tứ giác AEHF có
\(\widehat{AEH}=\widehat{AFH}=\widehat{FAE}=90^0\)
=>AEHF là hình chữ nhật
=>AH=EF
b: Ta có: AEHF là hình chữ nhật
=>HE//AF và HE=AF
Ta có: HE//AF
F\(\in\)AK
Do đó: HE//KF
Ta có: HE=AF
AF=FK
Do đó: HE=KF
Xét tứ giác HEFK có
HE//FK
HE=FK
Do đó: HEFK là hình bình hành
c: Ta có: AEHF là hình chữ nhật
=>AH cắt EF tại trung điểm của mỗi đường
=>O là trung điểm chung của AH và EF
Ta có: HEFK là hình bình hành
=>HF cắt EK tại trung điểm của mỗi đường
=>I là trung điểm chung của HF và ÊK
Xét ΔEKF có
O,I lần lượt là trung điểm của EF,EK
=>OI là đường trung bình của ΔEKF
=>OI//KF
=>OI//AC