Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
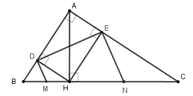
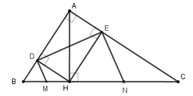
Gọi AM cắt DE tại I
Theo tính chất hình chữ nhật ADHE : \(\widehat{E_1}=\widehat{HAC}=\widehat{MBA};\widehat{A_1}=\widehat{D_1}=\widehat{AHE}=\widehat{MCA}\)
\(\Rightarrow\widehat{A_1}=\widehat{ACM}\Rightarrow\Delta ACM\)cân tại M \(\Rightarrow MA=MC\)(*)
Do \(\Delta AID\)vuông tại I suy ra
\(\widehat{DAM}+\widehat{D_1}=90^0\Leftrightarrow\widehat{DAM}+\widehat{DAH}=90^0\left(1\right)\)
\(\widehat{ABM}+\widehat{DAH}=90^0\left(2\right)\)
Từ (1) và (2) suy ra \(\widehat{DAM}=\widehat{ABM}\)
\(\Rightarrow\Delta ABM\)cân tại M \(\Rightarrow MA=MB\)(**)
Từ (*);(**) suy ra MB=MC hay M là trung điểm BC . Do MF//AC suy ra
\(\widehat{MFC}=\widehat{ACF}\)
Mà
\(\widehat{ACF}=\widehat{MCF}\Rightarrow\widehat{MFC}=\widehat{MCF}\Rightarrow\Delta MFC\)cân tại M suy ra MC=MF
Mà MB=MC suy ra 
\(\Delta BFC\) có FM là trung tuyến 
\(FM=\frac{1}{2}BC\Rightarrow\) \(\Delta BFC\)vuông tại F hay 
\(BF\perp CF\left(đpcm\right)\)
a: \(AB=\sqrt{3\cdot15}=3\sqrt{5}\left(cm\right)\)
\(AC=\sqrt{12\cdot15}=6\sqrt{5}\left(cm\right)\)
b: \(\dfrac{HF}{HE}=\dfrac{AE}{AF}=\dfrac{AH^2}{AB}:\dfrac{AH^2}{AC}=\dfrac{AC}{AB}=2\)
=>HF=2HE
Tứ giác AEHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 o nên DE = AH.
Xét ABC vuông tại A có: A H 2 = HB.HC = 9.16 = 144 => AH = 12
Nên DE = 12cm
Đáp án cần chọn là: A
Tứ giác ARHD là hình chữ nhật vì: A ^ = E ^ = D ^ = 90 ∘ nên DE = AH.
Xét ∆ ABC vuông tại A có A H 2 = HB.HC = 4.9 = 36 ⇔ AH = 6
Nên DE = 6cm
Đáp án cần chọn là : D