Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Theo hệ thức lượng trong tam giác vuông :
\(\Delta ABC\)có :\(BA'=\frac{AB^2}{BC};CA'=\frac{AC^2}{BC}\)
\(\Delta BDA\)có :\(BF=\frac{BA'^2}{AB}=\left(\frac{AB^2}{BC}\right)^2:AB=\frac{AB^3}{BC^2}\)
\(\Delta DAC\)có :\(CE=\frac{CA'^2}{AC}=\left(\frac{AC^2}{BC}\right)^2:AC=\frac{AC^3}{BC^2}\)
\(\Rightarrow\frac{CE}{BF}=\frac{AC^3}{BC^2}:\frac{AB^3}{BC^2}=\frac{AC^3}{AB^3}\)

góc ADH=góc AEH=góc DAE=90 độ
=>ADHE là hình chữ nhật
=>AH=DE
BD*CE*BC
=BH^2/BA*CH^2/CA*BC
=AH^4/AH=AH^3
=DE^3

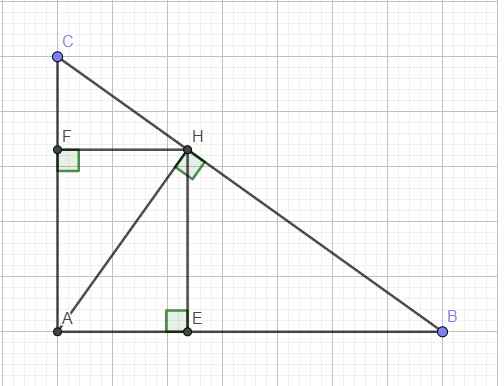
Tứ giác AEHF là hình chữ nhật (có 3 góc vuông) \(\Rightarrow HE=AF\)
Áp dụng định lý Pitago trong tam giác vuông AFH:
\(AH^2=AF^2+HF^2=HE^2+HF^2\)
Áp dụng hệ thức lượng trong tam giác vuông AHB với đường cao HF:
\(HF^2=AF.FC\)
Tương tự:
\(HE^2=AE.EB\)
\(\Rightarrow AH^2=HE^2+HF^2=AE.EB+AF.FC\) (đpcm)

bạn tự vẽ hình nha
áp dụng hệ thức lượng trong tam giác vuông ABCco \(AB^2=BA'^2\cdot BC,AC^2=A'C^2\cdot BC\)
\(\Rightarrow\frac{AB^2}{AC^2}=\frac{BA'}{A'C}\Rightarrow\frac{AC^4}{AB^4}=\frac{A'C^2}{A'B^2}\) (1)
mà trong tam giác vuông AA'B có\(BA'^2=BF\cdot AB\)
trong tam giác vuông AA'C có \(A'C^2=EC\cdot AC\)
thay vào (1) ta co \(\frac{AC^4}{AB^4}=\frac{EC\cdot AC}{BF\cdot AB}\Rightarrow\frac{AC^3}{AB^3}=\frac{EC}{BF}\left(DPCM\right)\)
b,de dang chung minh duoc tam giac BMD~BAC
SUY RA \(\frac{BD}{BC}=\frac{BM}{BA}=\frac{MD}{AC}\) (2)
tuong tu tam giac NDC~ABC
SUY RA \(\frac{DC}{BC}=\frac{NC}{AC}=\frac{ND}{AB}\)(3)
nhan (2) voi (3) ta co \(\frac{BD\cdot DC}{BC^2}=\frac{BM\cdot ND}{AB^2}=\frac{MD\cdot NC}{AC^2}=\frac{BM\cdot ND+MD\cdot NC}{AB^2+AC^2}\)
suy ra \(BD\cdot DC=BM\cdot ND+MD\cdot NC\)
de dang cm duoc tu giac AMDN la hcn suy ra MA =ND,MD=AN
THAY VAO BIEU THUC TREN TA CO \(BD\cdot DC=MA\cdot MB+NA\cdot NC\left(DPCM\right)\)