Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=9^2+12^2=225\)
=>\(BC=\sqrt{225}=15\left(cm\right)\)
b: Xét ΔBAD vuông tại A và ΔBMD vuông tại M có
BD chung
\(\widehat{ABD}=\widehat{MBD}\)
Do đó: ΔBAD=ΔBMD
=>DA=DM
c: Xét ΔDAE vuông tại A và ΔDMC vuông tại M có
DA=DM
\(\widehat{ADE}=\widehat{MDC}\)(hai góc đối đỉnh)
Do đó: ΔDAE=ΔDMC
=>AE=MC
Ta có: ΔBAD=ΔBMD
=>BA=BM
Xét ΔBEC có \(\dfrac{BA}{AE}=\dfrac{BM}{MC}\)
nên AM//EC

a: Xét ΔABI và ΔACI có
AB=AC
góc BAI=góc CAI
AI chung
=>ΔABI=ΔACI
b: ΔABI=ΔACI
=>góc AIB=góc AIC
c: Xét tứ giác ABEC có
I là trung điểm chung của AE và BC
=>ABEC là hình bình hành
=>BE//AC

a)
Xét ΔAIB và ΔAID có:
Góc BAI= Góc DAI (gt)
AB=AD
AI chung
→ ΔAIB=ΔAID (c.g.c)
⇒ IB=ID (2 cạnh tương ứng)
b)
Vì góc AIB= góc AID (2 góc tương ứng)

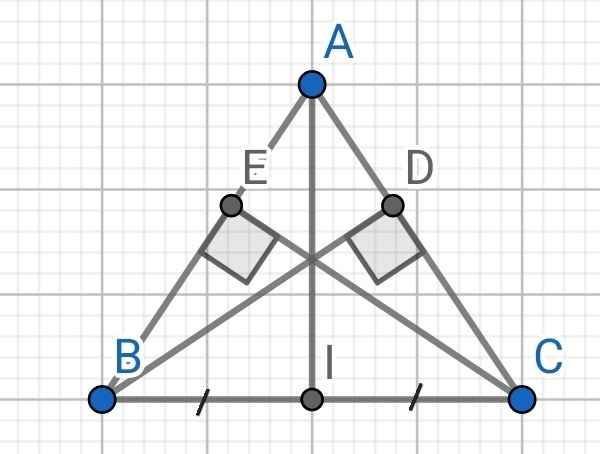 a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
a) Xét hai tam giác vuông: ∆ABD và ∆ACE có:
AB = AC (do ∆ABC cân tại A)
∠A chung
⇒ ∆ABD = ∆ACE (cạnh huyền - góc nhọn)
b) Do I là trung điểm của BC (gt)
⇒ IB = IC
Xét ∆ABI và ∆ACI có:
AB = AC (cmt)
AI là cạnh chung
BI = CI (cmt)
⇒ ∆ABI = ∆ACI (c-c-c)
⇒ ∠BAI = ∠CAI (hai góc tương ứng)
⇒ AI là tia phân giác của ∠BAC
c) Do ∆ABI = ∆ACI (cmt)
⇒ ∠AIB = ∠AIC (hai góc tương ứng)
Mà ∠AIB + ∠AIC = 180⁰ (kề bù)
⇒ ∠AIB = ∠AIC = 180⁰ : 2 = 90⁰
⇒ AI ⊥ BC

a) Hai tam giác vuông \(ABD\)và \(HBD\)có:
BD chung
\(\widehat{ABD}=\widehat{HBD}\)(BD là tia phân giác của \(\widehat{ABC}\))
\(\Rightarrow\Delta ABD=\Delta HBD\)(cạnh huyền - góc nhọn)
\(\Rightarrow AD=DH\)(hai cạnh tương ứng)
b) \(AD=DH\)(câu a) (1)
\(\Delta HDC\)vuông tại H
\(\Rightarrow DH< DC\) (2)
Từ (1) và (2) suy ra: \(AD< DC\)
c) \(\Delta ADK\)và\(\Delta HDC\)có:
\(\widehat{KAD}=\widehat{CHD}=90^0\)
\(AD=HD\left(\Delta ABD=\Delta HBD\right)\)
\(\widehat{ADK}=\widehat{HDC}\)(đối đỉnh)
\(\Rightarrow\Delta ADK=\Delta HDC\left(g.c.g\right)\)
\(\Rightarrow AK=HC\)(hai cạnh tương ứng)
\(BK=AB+AK\)
\(BC=HB+HC\)
Mà \(AB=HB\)và \(AK=HC\)
Nên \(BK=BC\)
\(\Rightarrow\Delta KBC\)cân tại \(B\)
a: \(BC=\sqrt{4^2+6^2}=2\sqrt{13}\left(cm\right)\)
b: Xét ΔABI vuông tại A và ΔDBI vuông tại D có
BI chung
\(\widehat{ABI}=\widehat{DBI}\)
Do đó: ΔABI=ΔDBI
c: Ta có: ΔABI=ΔDBI
nên IA=ID
d: Ta có: ΔABI=ΔDBI
nên \(\widehat{AIB}=\widehat{DIB}\)
hay IB là tia phân giác của góc AID
a. Áp dụng định lý pitago, ta có:
\(BC^2=AB^2+AC^2\)
\(\Rightarrow BC=\sqrt{4^2+6^2}=\sqrt{52}=2\sqrt{13}cm\)
b.c.d.Xét tam giác vuông ABI và tam giác vuông DBI, có:
góc ABI = góc DBI ( gt )
AI: cạnh chung
Vậy tam giác vuông ABI = tam giác vuông DBI ( cạnh huyền. góc nhọn )
=> IA = ID ( 2 cạnh tương ứng )
=> góc AIB = góc DIB ( 2 góc tương ứng )
=> IB là tia phân giác góc AID