Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: \(CB=\sqrt{12^2+16^2}=20\left(cm\right)\)
AH=12*16/20=9,6cm
Xet ΔABC có AD là phân giác
nên BD/AB=CD/AC
=>BD/3=CD/4=(BD+CD)/(3+4)=20/7
=>BD=60/7cm; CD=80/7cm
b: Sửa đề: AB,AC
Xét tứ giác AMHN có
góc AMH=góc ANH=góc MAN=90 độ
=>AMHN là hình chữ nhật
AM=AH^2/AB=9,6^2/12=7,68(cm)
AN=AH^2/AC=9,6^2/16=5,76(cm)
\(S_{AMHN}=7.68\cdot5.76=44.2368\left(cm^2\right)\)

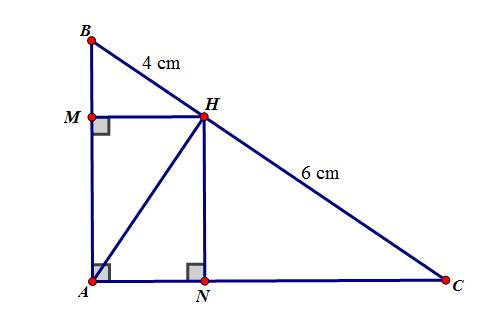
a, ΔABC vuông tại A \(\Rightarrow \angle BAC=90^o\)
M, N lần lượt là hình chiếu của H lên AB, AC \(\Rightarrow \angle HMA= \angle HNA =90^o \)
Tứ giác AMHN có: \(\angle BAC=\angle HMA=\angle HNA=90^o\)
Suy ra AMHN là hình chữ nhật.
b, Có: ΔAHB ∼ ΔCAB (g.g) \(\Rightarrow AB^2=BH.BC=4.(4+6)=40 \Rightarrow AB=2\sqrt{10}\)(cm)
Có: ΔAHC ∼ ΔBAC (g.g) \(\Rightarrow AC^2=CH.CB=6.(6+4)=60 \Rightarrow AC=2\sqrt{15}(cm)\)
SΔABC=\(\dfrac{1}{2}.AB.AC=\dfrac{1}{2}.2.\sqrt{10}.2.\sqrt{15}=10\sqrt{6}\)(cm2)

b, chứng minh tương tự câu a:
ΔAHN đồng dạng ΔACH ⇒AH/AC=AN/AH
⇒AH⊃2;=AN.AC
⇒AB.AM=AC.AN=AH⊃2;
xét ΔAMN và ΔACB có : góc A chung
AM.AB=AN.AC⇒AM/AN=AC/AB
⇒ΔAMN đồng dạng ΔACB

HN//AB
=>góc NHA=góc HAM
=>góc NHA=góc MHA
=>HA là phân giác của góc NHM
HC vuông góc HA
=>HC là phân giác ngoài của ΔIHN

a: góc AIH=góc AKH=góc KAI=90 độ
=>AIHK là hcn
b: AIHK là hcn
=>góc AIK=góc AHK=góc C
=>ΔAIK đồng dạng với ΔACB
sao lại cần M,N bạn nhỉ