Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

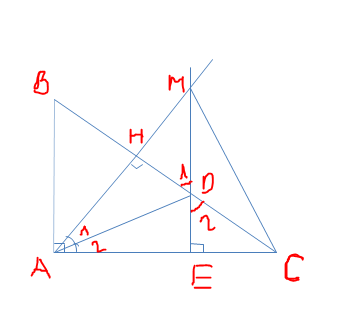
a/ Xét \(\Delta\) vuông AHD và \(\Delta\) AED. Có:
\(\widehat{A1}\)= \(\widehat{A2}\) ( giả thiết)
AD chung
=> \(\Delta AHD=\Delta AED\) ( ch-gn)
=> DH = DE ( 2 cạnh tương ứng )
b/ BMC không cân được bạn nhé. bạn chép nhầm đề bài r: Chứng minh DMC cân mới đúng.
Xét \(\Delta vuôngHDM\) và \(\Delta vuôngEDC\). Có:
\(\widehat{D1}\) = \(\widehat{D2}\) ( đối đỉnh)
HD = HE ( cmt)
=> \(\Delta HDM=\Delta EDC\left(cgv-gnk\right)\)
=> DM = DC ( 2 cạnh tương ứng)
=> Xét \(\Delta DMCcóDM=DC=>\Delta DMCcân\left(cântạiD\right)\)
~ Cậu ktra lại nhé~

a) ΔABDΔABD cân tại A => BADˆ=BDAˆBAD^=BDA^ (t/c tam giác cân)
Lại có: BADˆ+DAEˆ=BACˆ=90oBAD^+DAE^=BAC^=90o
BDAˆ+ADEˆ=BDEˆ=90oBDA^+ADE^=BDE^=90o
Do đó, DAEˆ=ADEˆDAE^=ADE^
=> ΔADEΔADE cân tại E (dấu hiệu nhận biết tam giác cân)
=> AE = ED (t/c tam giác cân) (đpcm)
a) Có: AH // ED (cùng ⊥BC⊥BC)
=> HADˆ=ADEˆHAD^=ADE^ (so le trong)
= DAE (câu a)
=> AD là phân giác HACˆ(đpcm)
