OLM cung cấp gói bải giảng điện tử PPT cho giáo viên đầu năm học

Thi thử và xem hướng dẫn giải chi tiết đề tham khảo 12 môn thi Tốt nghiệp THPT 2025

Tập huấn miễn phí ra đề kiểm tra và chấm phiếu trắc nghiệm dành cho giáo viên khối THCS

K
Khách

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
Mua vip
PT
Pham Trong Bach
12 tháng 5 2019
Cho tam giác ABC trọng tâm G,M là trung điểm BC. Trong các mệnh đề sau đây, mệnh đề nào sai : A. Phép vị tự tâm G tỉ số k = –2 biến điểm A thành điểm M. B.Phép vị tự tâm G tỉ số k = –2 biến điểm M thành điểm A C. Phép vị tự tâm A tỉ số k = 3 2  biến điểm G thành điểm M D. Phép vị tự tâm M tỉ số k = 1 3  biến điểm A thành điểm...
Đọc tiếp

Cho tam giác ABC trọng tâm G,M là trung điểm BC. Trong các mệnh đề sau đây, mệnh đề nào sai :

A. Phép vị tự tâm G tỉ số k = –2 biến điểm A thành điểm M.

B.Phép vị tự tâm G tỉ số k = –2 biến điểm M thành điểm A

C. Phép vị tự tâm A tỉ số k = 3 2  biến điểm G thành điểm M

D. Phép vị tự tâm M tỉ số k = 1 3  biến điểm A thành điểm G.
#Toán lớp 11
1
CM
Cao Minh Tâm
12 tháng 5 2019

Đáp án B

G A → = − 2 G M →

Đúng(0)
PT
Pham Trong Bach
19 tháng 9 2017
Cho một tam giác ABC đều tâm O. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng? A.  Q ( 0 ;   120 o ) ( ∆ O D C )   =   ∆ O F A B.  Q ( 0 ;   120 o ) ( ∆ A O F )   =   ∆ B O D C.  Q ( 0 ;   120 ...
Đọc tiếp

Cho một tam giác ABC đều tâm O. Gọi D, E, F lần lượt là trung điểm các cạnh BC, CA, AB. Mệnh đề nào sau đây đúng?

A.  Q ( 0 ;   120 o ) ( ∆ O D C )   =   ∆ O F A

B.  Q ( 0 ;   120 o ) ( ∆ A O F )   =   ∆ B O D

C.  Q ( 0 ;   120 o ) ( ∆ A O B )   =   ∆ A O C

D.  Q ( 0 ;   60 o ) ( ∆ O F E )   =   ∆ O D E

#Toán lớp 11
1
CM
Cao Minh Tâm
19 tháng 9 2017

Đúng(0)
B
Buddy
17 tháng 7 2023

Cho tam giác \(ABC\). Lấy điểm \(M\) trên cạnh \(AC\) kéo dài (Hình 1). Mệnh đề nào sau đây là mệnh đề sai?

A. \(M \in \left( {ABC} \right)\).

B. \(C \in \left( {ABM} \right)\).     

C. \(A \in \left( {MBC} \right)\).

D. \(B \in \left( {ACM} \right)\).
#Toán lớp 11
1
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023

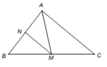
\(\left. \begin{array}{l}M \in AC\\AC \subset \left( {ABC} \right)\end{array} \right\} \Rightarrow M \in \left( {ABC} \right)\). Vậy mệnh đề A đúng.

\(\left. \begin{array}{l}C \in AM\\AM \subset \left( {ABM} \right)\end{array} \right\} \Rightarrow C \in \left( {ABM} \right)\). Vậy mệnh đề B đúng.

\(\left. \begin{array}{l}A \in CM\\CM \subset \left( {MBC} \right)\end{array} \right\} \Rightarrow A \in \left( {MBC} \right)\). Vậy mệnh đề C đúng.

Vậy mệnh đề D sai.

Chọn D.

Đúng(0)
PT
Pham Trong Bach
11 tháng 7 2019
Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai. A. T 1 / 2   B C → ( F )   =   E B . T D E → ( B )   =   F C. T 2 D G →   ( A )   =   G D. T 1 / 2   ...
Đọc tiếp

Cho tam giác ABC có trọng tâm G, Gọi D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB. Mệnh đề nào sau đây là sai.

A. T 1 / 2   B C → ( F )   =   E

B . T D E → ( B )   =   F

C. T 2 D G →   ( A )   =   G

D. T 1 / 2   G A → ( D )   =   G

#Toán lớp 11
1
CM
Cao Minh Tâm
11 tháng 7 2019

Đáp án C

Ta có: D, E, F lần lượt là trung điểm của các cạnh BC, CA, AB

Do đó: DE, EF, FD là các đường trung bình của tam giác ABC

Suy ra F E   //= 1 2 B C D E   //= 1 2 A B D F   //= 1 2 A C

Do đó ta có các phép tịnh tiến như sau: T 1 2 B C → F = E ; T D E → B = F

Lại có G là trọng tâm tam giác ABC nên ta có DG = 1/2GA

T 1 2 G A → D = G ; T 2 D G → G = A

Vậy đáp án A, B, D đúng và C sai.

Chọn đáp án C.

Đúng(0)
PT
Pham Trong Bach
17 tháng 3 2017

Cho tứ diện ABCD với G là trọng tâm của tam giác ABD, M là điểm trên cạnh BC sao cho . Khi đó mệnh đề nào sau đây là đúng? 

A. MG cắt CD.

B. MG//CD.

C. MG//(ACD)

D. MG cắt BD.
#Toán lớp 11
1
CM
Cao Minh Tâm
17 tháng 3 2017

Đáp án C

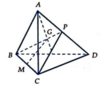
Gọi P là trung điểm của AD

=> MG // CP => MG // (ACD)

Đúng(0)
PT
Pham Trong Bach
19 tháng 3 2019
Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng? A. M G   ∥   (   B C D ) B.  M G   ∥   ( A C D ) C.  M G   ∥   ( A B D ) D.  M G   ∥   ( A B C ) ...
Đọc tiếp

Cho tứ diện ABCD. Gọi G là trọng tâm tam giác ABD, M là điểm thuộc cạnh BC sao cho MB = 2MC. Mệnh đề nào sau đây đúng?

A. M G   ∥   (   B C D )

B.  M G   ∥   ( A C D )

C.  M G   ∥   ( A B D )

D.  M G   ∥   ( A B C )

#Toán lớp 11
1
CM
Cao Minh Tâm
19 tháng 3 2019

Đúng(0)
PT
Pham Trong Bach
16 tháng 4 2019
Cho hình chóp S.ABC có đáy ABC là tam giác cân tại C, (SAB) ⊥ (ABC), SA = SB, I là trung điểm AB. Mệnh đề nào sau đây sai: A. Góc giữa    (SAB) và    (ABC) là góc SIC ...
Đọc tiếp

Cho hình chóp S.ABC có đáy ABC là tam giác cân tại C, (SAB) ⊥ (ABC), SA = SB, I là trung điểm AB. Mệnh đề nào sau đây sai:

A. Góc giữa    (SAB) và    (ABC) là góc SIC
#Toán lớp 11
1
CM
Cao Minh Tâm
16 tháng 4 2019

Đúng(0)
PT
Pham Trong Bach
25 tháng 4 2019
Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng? A. B. C. ...
Đọc tiếp

Cho tam giác ABC đều cạnh a. Mệnh đề nào sau đây đúng?

A.

B.

C. 

D. 
#Toán lớp 11
1
CM
Cao Minh Tâm
25 tháng 4 2019

Độ dài các cạnh của tam giác là a thì độ dài các vectơ

Chọn C

Đúng(0)
B
Buddy
17 tháng 7 2023

Cho tứ diện \(ABCD\) với \(I\) và \({\rm{?}}\) lần lượt là trung điểm các cạnh \(AB\) và \(CD\). Mệnh đề nào sau đây đúng?

A. Bốn điểm \(I,J,B,C\) đồng phẳng.

B. Bốn điểm \(I,J,A,C\) đồng phẳng.

C. Bốn điểm \(I,J,B,D\) đồng phẳng.

D. Bốn điểm \(I,J,C,D\) đồng phẳng.
#Toán lớp 11
1
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023

Ta có:

\(\left. \begin{array}{l}J \in C{\rm{D}}\\C{\rm{D}} \subset \left( {IC{\rm{D}}} \right)\end{array} \right\} \Rightarrow J \in \left( {IC{\rm{D}}} \right)\).

Vậy bốn điểm \(I,J,C,D\) đồng phẳng.

Chọn D.

Đúng(0)
Bảng xếp hạng
Tất cả Toán Vật lý Hóa học Sinh học Ngữ văn Tiếng anh Lịch sử Địa lý Tin học Công nghệ Giáo dục công dân Âm nhạc Mỹ thuật Tiếng anh thí điểm Lịch sử và Địa lý Thể dục Khoa học Tự nhiên và xã hội Đạo đức Thủ công Quốc phòng an ninh Tiếng việt Khoa học tự nhiên
  • Tuần
  • Tháng
  • Năm
Các khóa học có thể bạn quan tâm
Tổng thanh toán: 0đ (Tiết kiệm: 0đ)
Tới giỏ hàng
Yêu cầu VIP