Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)Gọi K là trung điểm của AI thì AK =KI (1)
Xét tam giác ADI có: B là trung điểm của AD(gt) và K là trung điểm của AI
Do đó: BK là đường trung bình của tam giác ADI =>: BK song song với DI và BK =1/2 DI (3)
Có: BK song song với MI (cmt) và M là trung điểm của BC nên I là trung điểm của CK thì IC = IK (2)
Từ (1),(2) suy ra: AK = KI = IC = 1/3 AC
Vậy AI =AK +KI = 2/3 AC = 2 IC

a: \(BC=\sqrt{6^2+8^2}=10\left(cm\right)\)
\(S_{ABC}=\dfrac{1}{2}\cdot6\cdot8=24\left(cm^2\right)\)
b: Xét tứ giác ADME có
góc ADM=góc AEM=góc DAE=90 độ
nên ADME là hình chữ nhật
c: Xét ΔABC có
M là trung điểm của BC
ME//AB
Do đó E là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MD//AC
Do đó: D là trung điểm của AB
=>ME//BD và ME=BD
=>MEDB là hình bình hành
=>MD cắtEB tại trung điểm của mỗi đường
=>B,K,E thẳng hàng

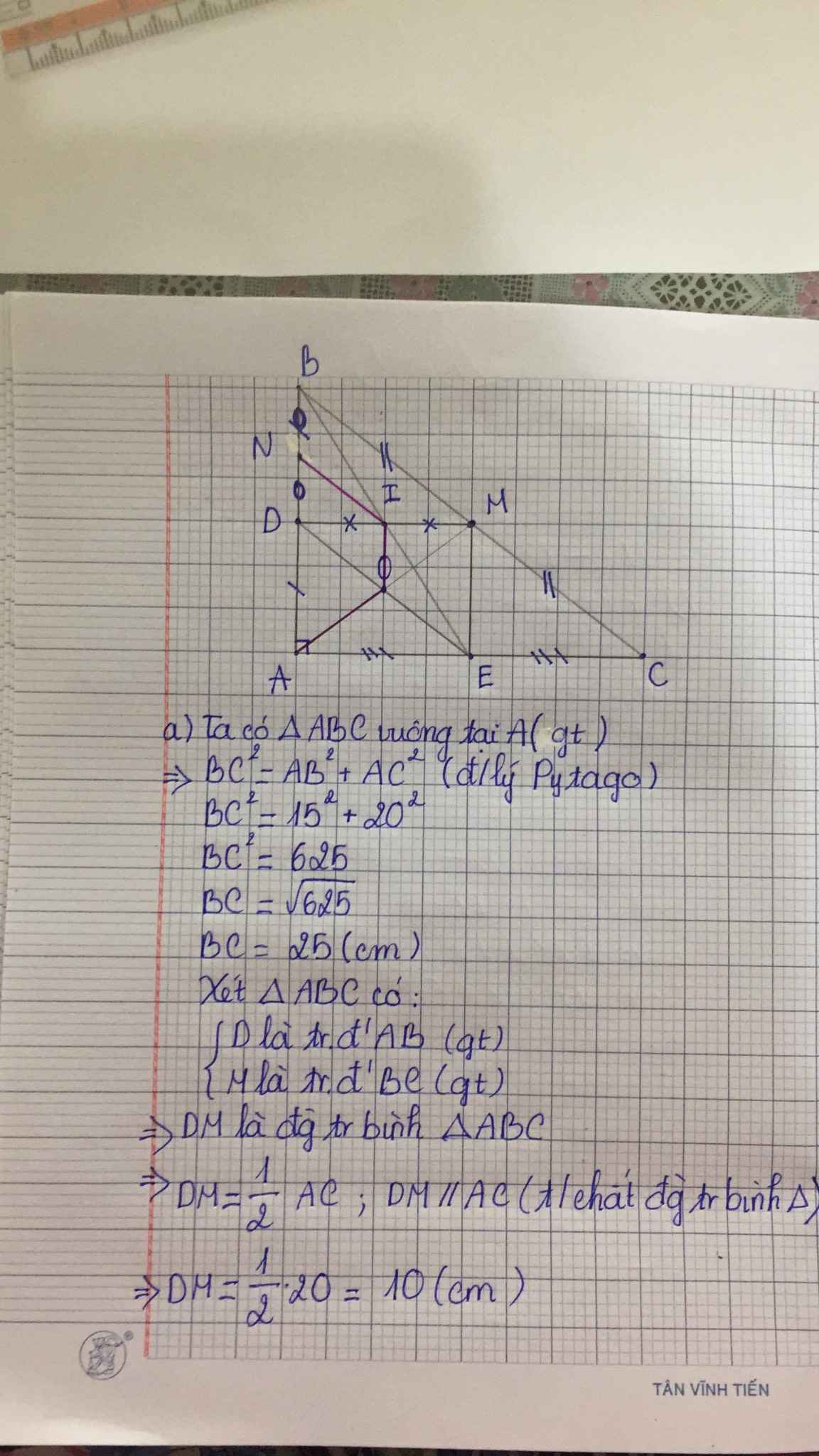
a: Xét ΔABC vuông tại A có \(BC^2=AB^2+AC^2\)
hay BC=25(cm)
Xét ΔABC có
D là trung điểm của AB
M là trung điểm của BC
Do đó: DM là đường trung bình của ΔABC
Suy ra: \(DM=\dfrac{AC}{2}=10\left(cm\right)\)

a: Xét tứ giác AEDF có
\(\widehat{AED}=\widehat{AFD}=\widehat{FAE}=90^0\)
Do đó: AEDF là hình chữ nhật

Bài 3:
a: Xét ΔAIB và ΔCID có
IA=IC
góc AIB=góc CID
IB=ID
Do đó: ΔAIB=ΔCID
b: Xét tứ giác ABCD có
I là trung điểm chung của AC và BD
nên ABCD là hình bình hành
Suy ra: AD//BC va AD=BC
Bài 6:
a: Xét ΔADB và ΔAEC có
AD=AE
góc A chung
AB=AC
Do đó: ΔADB=ΔAEC
SUy ra: BD=CE
b: Xét ΔEBC và ΔDCB có
EB=DC
BC chung
EC=BD
Do đó: ΔEBC=ΔDCB
Suy ra: góc OBC=góc OCB
=>ΔOBC cân tại O
=>OB=OC
=>OE=OD
=>ΔOED cân tại O
c: Xét ΔABC có AE/AB=AD/AC
nên ED//BC

Gọi K là trung điểm của AI thì AK =KI (1)
Xét tam giác ADI có: B là trung điểm của AD(gt) và K là trung điểm của AI (cách vẽ)
Do đó: BK là đường trung bình của tam giác ADI suy ra:
BK song song với DI và BK =1/2 DI (3)
Tam giác KBC có: BK song song với MI (cmt) và M là trung điểm của BC
Nên I là trung điểm của CK thì IC = IK (2)
Từ (1),(2) suy ra: AK = KI = IC = 1/3 AC
Vậy AI =AK +KI = 2/3 AC = 2 IC
b, Tam giác KBC có: MI là đường trung bình của tam giác KBC nên MI =1/2 BK (4)
TỪ (3) và (4) suy ra: MI =1/4 DI
Vì điểm M nằm giữa 2 điểm D và I nên:
MI + MD = DI
1/4 DI + MD = DI
MD = 3/4 DI
Ta có: MD =3/4 DI và MI=1/4 DI
Do đó: MD = 3MI