Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, Sử dụng định lí Pytago cho các tam giác vuông HAB và HAC để có đpcm
b, 1. Chứng minh tương tự câu a)
2. Sử dụng định lí Pytago cho tam giác vuông AHM
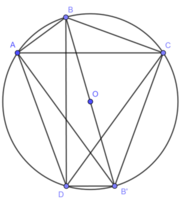
Kẻ đường kính BB’. Nối B’A, B’D, B’C.
Ta có: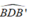
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ AC // B'D ( cùng vuông góc với BD)
Suy ra, tứ giác ADB’C là hình thang
Vì ADB’C nội tiếp đường tròn (O) nên ADB’C là hình thang cân
⇒ CD = AB'
⇒ A B 2 + C D 2 = A B 2 + A B ' 2
Mà tam giác BAB’ vuông tại A do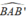 
= 90° ( góc nội tiếp chắn nửa đường tròn)
⇒ A B 2 + C D 2 = A B 2 + A B ' 2 = 2 R 2 = 4 R 2 (đpcm)
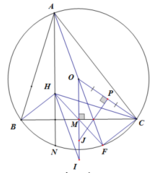
b) Vì AHIO là hình bình hành nên OI = AH = 2OM
Gọi P là trung điểm OC ⇒ PJ là trung trực OC ⇒ PJ ⊥ OC.
Có OM là trung trực BC ⇒ OM ⊥ BC. Suy ra
Δ O J P ~ Δ O C M ( g . g ) ⇒ O J O C = O P O M ⇒ O J . O M = O C . O P ⇒ O J .2 O M = O C .2 O P ⇒ O J . O I = O C . O C = R 2
Kẻ đường cao BH
Xét tam giác ABH vuông tại H có ∠(BAC) = 60 0
BH = AB.sin A = AB.sin 60 0 = (AB 3 )/2
AH = AB.cos A = AB.cos 60 0 = AB/2
Xét tam giác BHC vuông tại H có:
B C 2 = B H 2 + H C 2 = B H 2 + A C - A H 2
= B H 2 + A C 2 - 2 A C . A H + A H 2
Vậy được điều phải chứng minh.