Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải :
Ta có : \(\frac{AB'}{AB}=\frac{AC'}{AC}\)( GT ) ( 1 )
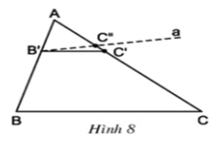
+) Đường thẳng a đi qua B' song song với BC ( GT )
\(B'C''//BC\)( vì đường thẳng a cắt AC tại C'' )
\(\Rightarrow\frac{AB'}{AB}=\frac{AC''}{AC}\)( Định lí Ta lét ) ( 2 )
Từ ( 1 ) và ( 2 )
\(\Rightarrow AC'=AC''\)

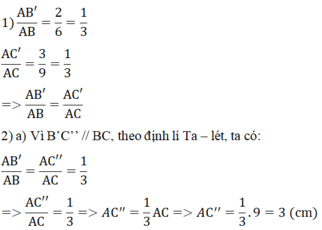
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

a) Ta có:
\(\frac{{AB'}}{{AB}} = \frac{2}{6} = \frac{1}{3}\) và \(\frac{{AC'}}{{AC}} = \frac{5}{{15}} = \frac{1}{3}\).
b) Vì \(B'E//BC\) và\(B'E\) cắt \(AC\) tại \(E\) nên theo định lí Thales ta có:
\(\frac{{AB'}}{{AB}} = \frac{{AE}}{{AC}} \Rightarrow \frac{2}{6} = \frac{{AE}}{{15}} \Rightarrow AE = \frac{{2.15}}{6} = 5cm\)
c) Ta có: \(AE = AC' = 5cm\).
d) Điểm \(E \equiv C'\) và đường thẳng \(B'C' \equiv B'E\).
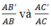
Akai HarumaAkai HarumaAkai HarumaAkai HarumaAkai Haruma
Phạm Minh QuangAkai HarumaNguyễn Lê Phước ThịnhHồng Phúc
Thiên ThảoHATHACO HATHACOPhạm Thái DươngNguyễn Văn ToànSky SơnTùngMiyuki MisakiCuc PhamWhite Hold??_Trang_??
Linh Nguyen