Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

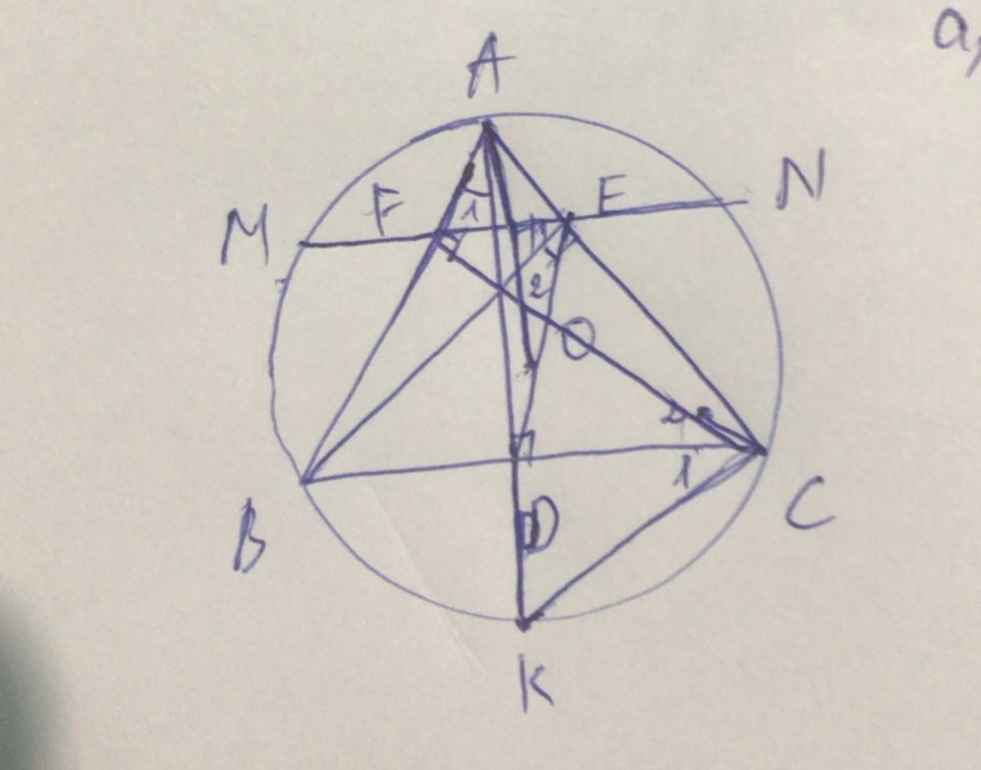
a: Xét tứ giác BDEA có
góc BDA=góc BEA=90 độ
=>BDEA là tứ giác nội tiếp
b: Kẻ tiếp tuyến Ax
=>góc xAC=góc ABC
mà góc ABC=góc AEF(=180 độ-góc FEC)
nên góc xAC=góc AEF
=>Ax//FE
=>FE vuông góc OA
Xét (O) có
ΔACA' nội tiếp
AA' là đường kính
=>ΔACA' vuông tại C
Xét tứ giác A'CEM có
góc EMA'+góc ECA'=180 độ
=>A'CEM là tứ giác nội tiếp

Gọi I,T lần lượt là trung điểm HF, EF. Ta có \(\Delta FHD~\Delta FEC\)(g.g), trung tuyến tương ứng là DI,CT
Suy ra \(\widehat{ECT}=\widehat{HDI}\). Vì DI là đường trung bình \(\Delta HMF\) nên \(\widehat{HDI}=\widehat{HMF}=\widehat{ACQ}\)
Do đó \(\widehat{ECT}=\widehat{ACQ}\), suy ra C,T,Q thẳng hàng. Tương tự B,T,P thẳng hàng.
Mặt khác, theo một kết quả quen thuộc thì tứ giác EHFR điều hòa, suy ra RH là đường đối trung của \(\Delta REF\)
Lại có HS || EF vì cùng vuông góc OA. Suy ra (HF = (SE hay H,S đẳng giác trong \(\widehat{ERF}\)
Suy ra RS là trung tuyến của \(\Delta REF\) hay RS đi qua T.
Vậy RS,BP,CQ cùng đi qua T.