



Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.






B1, a, Xét tứ giác AEHF có: góc AFH = 90o ( góc nội tiếp chắn nửa đường tròn)
góc AEH = 90o (góc nội tiếp chắn nửa đường tròn )
Góc CAB = 90o ( tam giác ABC vuông tại A)
=> tứ giác AEHF là hcn(đpcm)
b, do AEHF là hcn => cũng là tứ giác nội tiếp => góc AEF = góc AHF ( hia góc nội tiếp cùng chắn cung AF)
mà góc AHF = góc ACB ( cùng phụ với góc FHC)
=> góc AEF = góc ACB => theo góc ngoài tứ giác thì tứ giác BEFC là tứ giác nội tiếp (đpcm)
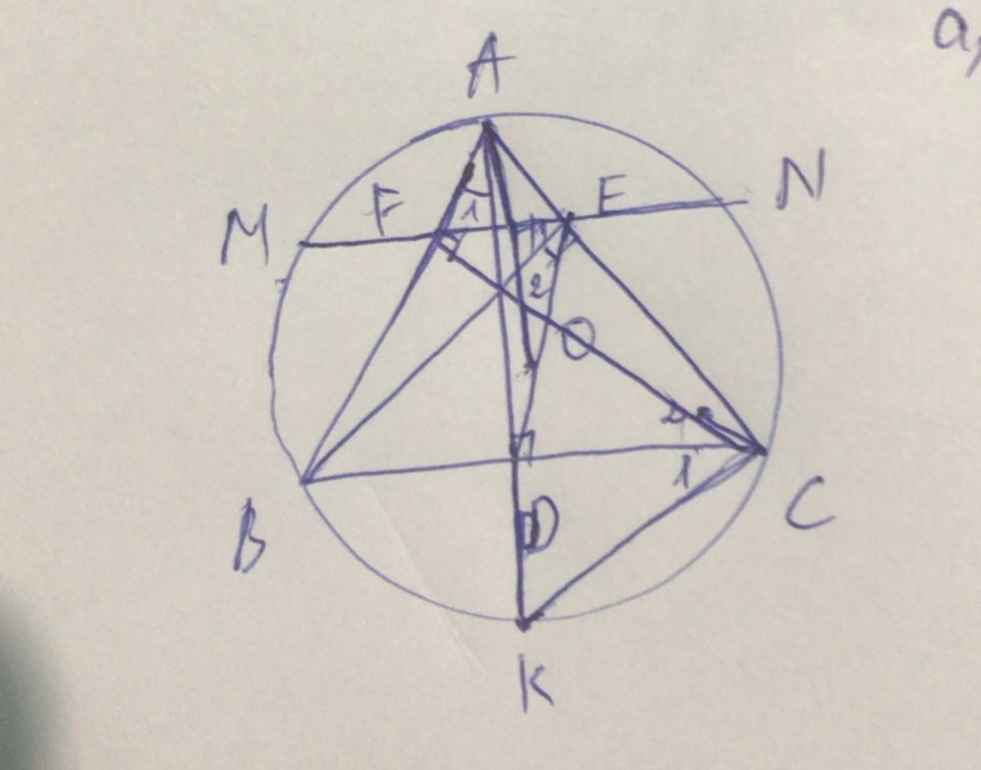
c,gọi M là giao điểm của AI và EF
ta có:góc AEF = góc ACB (c.m.t) (1)
do tam giác ABC vuông tại A và có I là trung điểm của cạng huyền CB => CBI=IB=IA
hay tam giác IAB cân tại I => góc MAE = góc ABC (2)
mà góc ACB + góc ABC + góc BAC = 180o (tổng 3 góc trong một tam giác)
=> ACB + góc ABC = 90o (3)
từ (1) (2) và (3) => góc AEF + góc MAE = 90o
=> góc AME = 90o (theo tổng 3 góc trong một tam giác)
hay AI uông góc với EF (đpcm)

Bài 1:
+) Chứng minh tứ giác BFLK nội tiếp:
Ta thấy FAH và LAH là hai tam giác vuông có chung cạnh huyền AH nên AFHL là tứ giác nội tiếp. Vậy thì \(\widehat{ALF}=\widehat{AHF}\) (Hai góc nội tiếp cùng chắn cung AF)
Lại có \(\widehat{AHF}=\widehat{FBK}\) (Cùng phụ với góc \(\widehat{FAH}\) )
Vậy nên \(\widehat{ALF}=\widehat{FBK}\), suy ra tứ giác BFLK nội tiếp (Góc ngoài tại một đỉnh bằng góc trong của đỉnh đối diện)
+) Chứng minh tứ giác CELK nội tiếp:
Hoàn toàn tương tự : Tứ giác AELH nội tiếp nên \(\widehat{ALE}=\widehat{AHE}\) , mà \(\widehat{AHE}=\widehat{ACD}\Rightarrow\widehat{ALE}=\widehat{ACD}\)
Suy ra tứ giác CELK nội tiếp.

Lời giải:
a) Vì $SB, SC$ là tiếp tuyến $(O)$ nên $SB\perp OB, SC\perp OC$
$\Rightarrow \widehat{OBS}=\widehat{OCS}=90^0$
Tứ giác $SBOC$ có tổng 2 góc đối nhau $\widehat{OBS}+\widehat{OCS}=90^0+90^0=180^0$ nên $SBOC$ là tứ giác nội tiếp.
b)
$\widehat{BEC}=\widehat{BFC}=90^0$ và cùng nhìn cạnh $BC$ nên $BFEC$ là tứ giác nội tiếp
$\Rightarrow \widehat{IFB}=\widehat{AFE}=\widehat{ACB}(1)$
Mà:
$\widehat{IBF}=\widehat{IBA}=\widehat{ACB}(2)$ (góc nt tạo bởi tiếp tuyến và dây cung thì bằng góc nội tiếp chắn cung đó)
Từ $(1);(2)\Rightarrow \widehat{IFB}=\widehat{IBF}$
$\Rightarrow \triangle IFB$ cân tại $I$
$\Rightarrow IF=IB$
c)
$\widehat{FAK}=\widehat{BAO}=\frac{180^0-\widehat{AOB}}{2}=90^0-\widehat{ACB}=\widehat{CAD}(3)$
$\widehat{AFK}=\widehat{AFE}=\widehat{ACB}=\widehat{ACD}(4)$
Từ $(3);(4)\Rightarrow \triangle AFK\sim \triangle ACD$ (g.g)
$\Rightarrow \frac{AF}{AC}=\frac{FK}{CD}(*)$
Mặt khác:
Dễ thấy $\triangle AFE\sim \triangle ACB$ (g.g)
$\Rightarrow \frac{AF}{AC}=\frac{FE}{CB}(**)$
Từ $(*);(**)\Rightarrow \frac{FK}{CD}=\frac{EF}{BC}$
$\Rightarrow FK.BC=EF.CD$ (đpcm)