Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác AEID có
\(\widehat{AEI}+\widehat{ADI}+\widehat{EAD}+\widehat{EID}=360^0\)
=>\(\widehat{EAD}+\widehat{EID}+90^0+90^0=360^0\)
=>\(\widehat{EAD}+\widehat{EID}=360^0-180^0=180^0\)
mà \(\widehat{EID}=\widehat{BIC}\)(hai góc đối đỉnh)
nên \(\widehat{EAD}+\widehat{BIC}=180^0\)
=>góc BIC bù với góc BAC

Bài 1:
Cách 1: Do điểm I nằm trong tam giác ABC nên: IBC<ABC và ICB<ACB
Cộng vế theo vế của chúng ta suy ra ABC+ACB>IBC+ICB
Do đó: 180-(ABC+ACB)<180-(IBC+ICB)
Tức là BAC<BIC và cũng là điều phải chứng minh
Cách 2:
Gọi D là giao điểm của BI với AC
Do BIC là góc ngoài của tam giác ICD nên BIC>BDC
Đồng thời BDC cũng là góc ngoài của tam giác ABD nên BDC >BAC
Do vậy BIC>BAC cũng là điều phải chứng minh
Bài 2
a)
Do BIC=180-IBC-ICB=180-1/2(B+C)=90+A nên BIC luôn lớn hơn 90
Mà BIC+CID=180=>CID=180-BIC<180-90=90
Thế nên CID là góc nhọn
b)
Từ giả thiết góc DIC=60 ta suy ra BIC=120=>IBC+ICB=60=>1/2(B+C)=60
Ta có:BEC+BDC=180-B-1/2C+180-C-1/2B
=360-(B+C)-1/2(B+C)
=360-120-60=180
Do vậy 2 góc BEC và BDC bù nhau

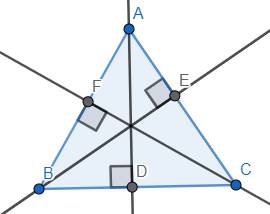
Nhận xét: AD, BE và CF là các đường cao, chúng đồng quy tại một điểm.
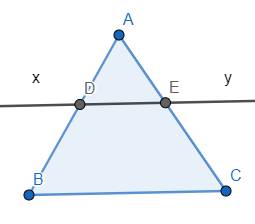
Dễ dàng thấy được \(\widehat{ABC}=\widehat{ADE}\) và \(\widehat{ACB}=\widehat{AED}\) (vì với mỗi cặp thì hai góc của cặp đó là hai góc so le trong)
Vì \(\widehat{ADE}\) và \(\widehat{BDE}\) là hai góc kề bù nên \(\widehat{ADE}+\widehat{BDE}=180^o\)
Mà \(\widehat{ABC}=\widehat{ADE}\) nên \(\widehat{ABC}+\widehat{BDE}=180^o\), suy ra \(\widehat{ABC}\) và \(\widehat{BDE}\) là hai góc bù nhau.
Suy luận tương tự như trên, ta được \(\widehat{ACB}\) và \(\widehat{CED}\) là hai góc bù nhau.

Xét tam giác ABC có:
^A+^B+^C=180°(đl tổng ba góc tam giác)
=>^B+^C=180°-a
Vì BI là pg ^B
=>^ABI=^IBC=1/2^B
Vì CI là pg ^C
=>^BCI=^ICA=1/2^C
Ta có:^B+^C=180°-a
=>(^B+^C)/2=(180°-a)/2
=>^IBC+^BCI=90°-a/2
Xét tam giác BIC có:
^IBC+^BCI+^BIC=180°(đl tổng ba góc tam giác)
=>^BIC=180°-90°-a/2
=>^BIC=90°+a/2
Bạn vẽ hình giúp mình nhé. Mình chỉ giải thôi nha!
1.Vì AH vuông góc với BC
=>^AHC=90°
Xét tam giác HAC vuông tại H
=>^HAC+^C=90°
=>^HAC=90° -^C (1)
Xét tam giác ABC vuông tại A
=>^B+^C=90°
=>^B=90° - ^C (2)
Từ (1) và (2)=>đpcm
-----------------------------------------------------------------
Câu này cm tương tự
mình ko biết vẽ à nhưng mình giải được cau hoi nay đó