Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

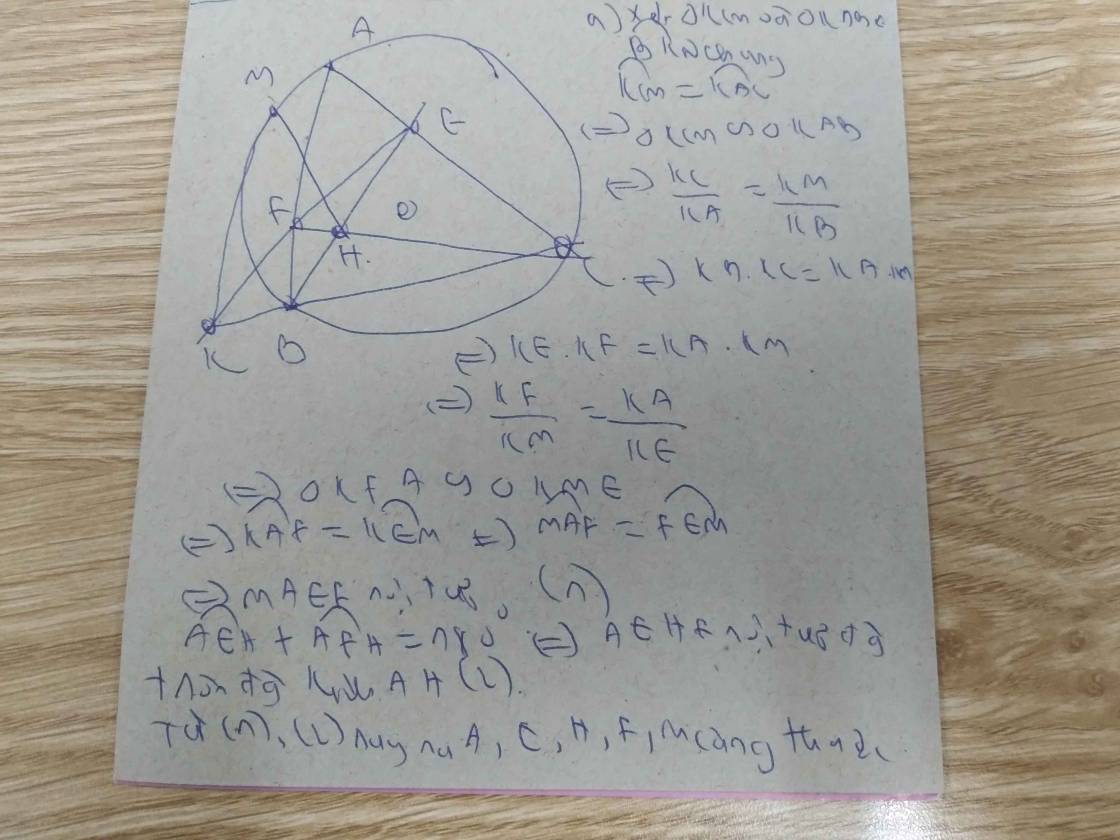
a) Xét tứ giác AEHF có \(\widehat{AEH}+\widehat{AFH}=90^o+90^o=180^o\)
=> AEHF là tứ giác nt
b) Xét tứ giác BCEF có 2 góc \(\widehat{BFC}\)và \(\widehat{CEB}\)cùng nhìn đoạn BC một góc 90o
=> BCEF là tứ giác nt
=> \(\widehat{KBF}=\widehat{KEC}\)(cùng bù với \(\widehat{FBC}\))
Xét \(\Delta KBF\)và \(\Delta KEC\)có
\(\widehat{KBF}=\widehat{KEC}\)
\(\widehat{CKE}\)chung
=> \(\Delta KBF\)ᔕ \(\Delta KEC\)(g-g)
=> \(\frac{KB}{KE}=\frac{KF}{KC}\)
=> KB . KC = KE . KF (1)
c) Nối M với B
Xét (O) có tứ giác AMBC nội tiếp đường tròn đó
=> \(\widehat{KBM}=\widehat{KAB}\)
Xét \(\Delta KBM\)và \(\Delta KAC\)có
\(\widehat{KBM}=\widehat{KAC}\)
\(\widehat{AKC}\)chung
=> \(\Delta KBM\)ᔕ \(\Delta KAC\)(g.g)
=> \(\frac{KB}{KA}=\frac{KM}{KC}\)=> KB . KC = KA . KM (2)
Từ (1) (2) => KE . KF = KA . KM
=> \(\frac{KF}{KA}=\frac{KM}{KE}\)
Xét \(\Delta KFMvà\Delta KAE\)có
\(\widehat{AFE}\)chung
\(\frac{KF}{KA}=\frac{KM}{KE}\)
=> \(\Delta KFM\)ᔕ \(\Delta KAE\)(g-g) <=> \(\widehat{KMF}=\widehat{KEA}\)hay \(\widehat{KMF}=\widehat{FEA}\)
Xét tứ giác AMFE có \(\widehat{KMF}=\widehat{FEA}\)=> AMFE là tứ giác nội tiếp
=> A, M, F ,E cùng thuộc một đường tròn
Mà A, F, H,E cùng thuộc một đường tròn (AFHE là tgnt)
=> A,F,M,H,E cùng thuộc một đường tròn
=> AMHE là tứ giác nt
=> \(\widehat{AMH}+\widehat{AEH}=180^o\)=> \(\widehat{AMH}=180^o-\widehat{AEH}=180^o-90^o=90^o\)
=> \(MH\perp AK\)
PHẦN D NGHĨ SAU NHÉ
d) À mik có ghi thiếu. Câu d c/m: MH cố định khi A di chuyển trên cung lớn BC

từ điểm O nằm ngoài đương tròn vẽ hai tiếp tuyến AB và AC vẽ dây BD song song AC AD cắt tại K tia BK cắt AC tại I
chứng minh IC bình =IK.IB
tam giácBAI đồng dạng tam giác AKI
i là trung điểm ac
tìm vị trí A để CK vuông góc AB

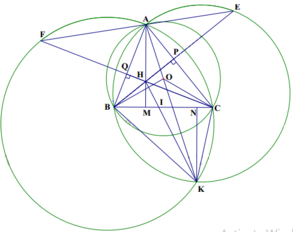
Ta có BOC=120o ;BKC =60o suy ra BOC +BKC =1800 nên tứ giác BOCK nội tiếp đường tròn.
Ta có OB=OC=R suy ra OB= OC=> BKO= CKO hay KO là phân giác góc BKC theo phần (a) KA

b) \(\widehat{NAB}=\widehat{AFE}=\widehat{ACB}\) nên NA là tiếp tuyến của (O).
Do O, N nằm trên đường trung trực của AB nên A, B đối xứng với nhau qua ON.
Từ đó NB là tiếp tuyến của (O).
c) Do NA là tiếp tuyến của (O) nên \(\Delta NAL\sim\Delta NKA(g.g)\)
\(\Rightarrow\dfrac{NA}{NK}=\dfrac{AL}{KA}=\dfrac{NL}{NA}\Rightarrow\left(\dfrac{AL}{KA}\right)^2=\dfrac{NA}{NK}.\dfrac{NL}{NA}=\dfrac{NL}{NK}\).
Tương tự do NB là tiếp tuyến của (O) nên \(\left(\dfrac{BL}{KB}\right)^2=\dfrac{NL}{NK}\Rightarrow\left(\dfrac{AL}{KA}\right)^2=\left(\dfrac{BL}{KB}\right)^2\Rightarrow\dfrac{AL}{KA}=\dfrac{BL}{KB}\Rightarrow\dfrac{AL}{BL}=\dfrac{KA}{KB}=\dfrac{2R}{KB}\).
Từ đó \(\dfrac{BK.AL}{BL}=2R\) không đổi \(\).
Sửa lại đề là đường tròn (HDS) đi qua một điểm cố định.
Ta có \(\widehat{ASE}=\widehat{EAS}=\widehat{OCA}\) nên tứ giác OECS nội tiếp. Từ đó \(AO.AS=AE.AC=AH.AD\). Suy ra tứ giác OHDS nội tiếp nên đường tròn ngoại tiếp tam giác HDS đi qua O cố định

a: góc BFC=góc BEC=90 độ
=>BCEF nội tiếp
b: Xét ΔKFB và ΔKCE có
góc KFB=góc KCE
góc K chung
=>ΔKFB đồng dạng với ΔKCE
=>KF/KC=KB/KE
=>KF*KE=KB*KC