Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Câu hỏi của Ngô Hà Minh - Toán lớp 9 - Học toán với OnlineMath

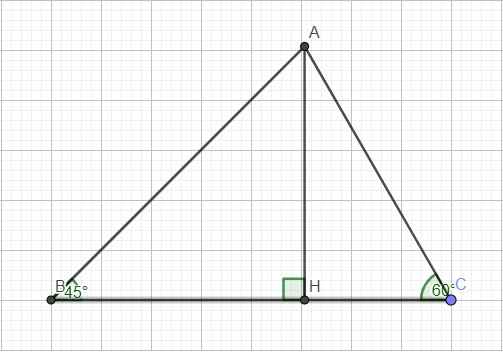
Kẻ đường cao AH ứng với BC
Trong tam giác vuông ABH ta có:
\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)
Trong tam giác vuông ACH ta có:
\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)
\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)
\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)
\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\)
\(\Rightarrow S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\dfrac{BC^2}{cotB+cotC}=\dfrac{\left(2a\right)^2}{2\left(cot45^0+cot60^0\right)}=\left(3-\sqrt{3}\right)a^2\)

a) Kẻ đường cao BK
Ta có:
\(\sin\widehat{A}=\frac{BK}{AB};\cos\widehat{A}=\frac{AK}{AB}\)
=> \(\sin\widehat{A}+\cos\widehat{A}=\frac{BK}{AB}+\frac{AK}{AB}=\frac{AK+BK}{AB}>\frac{AB}{AB}=1\)
b) Kẻ đường cao AH.
Đặt BH = x => HC = a - x.
+) Tam giác AHB vuông cân => AH = BH =x (1)
+) Tam giác AHC có \(\tan\widehat{ACH}=\frac{AH}{HC}\Rightarrow\tan60^o=\frac{AH}{a-x}\Rightarrow AH=\sqrt{3}\left(a-x\right)\) (2)
Từ (1) ; (2) => \(x=\sqrt{3}\left(a-x\right)\Rightarrow x=\frac{\sqrt{3}a}{1+\sqrt{3}}\)
=> \(AH=\frac{\sqrt{3}a}{1+\sqrt{3}}\)
=> \(S_{\Delta ABC}=\frac{1}{2}AH.BC=\frac{1}{2}.\frac{\sqrt{3}a}{1+\sqrt{3}}.a=\frac{3-\sqrt{3}}{4}a^2\)

Bài 2:
b: \(AH\cdot\left(\cot\widehat{B}+\cot\widehat{C}\right)\)
\(=AH\cdot\left(\dfrac{BH}{AH}+\dfrac{CH}{AH}\right)\)
\(=AH\cdot\dfrac{BC}{AH}=BC\)

bạn tự vẽ hình nha thông cảm cho mình
a) vẽ đường cao BH (BH⊥AC,H∈AC)
Ta có : \(\sin A+\cos A=\frac{BH}{AB}+\frac{AH}{AB}\)\(\left(\sin A=\frac{BH}{AB},\cos A=\frac{AH}{AB}\right)\)
\(\Leftrightarrow\sin A+\cos A=\frac{BH+AH}{AB}\)
Xét tam giác AHB ta có : \(BH+AH>AB\) (BĐT tam giác)
\(\Leftrightarrow\)\(\frac{BH+AH}{AB}>1\)
\(\Leftrightarrow\sin A+cosA>1\)(đpcm)
b)Ta có :\(\cot B=\frac{BH}{AH},\cot C=\frac{HC}{AH},BH+HC=BC\)
VP:\(AH\cdot\left(\cot B+\cot C\right)\)
\(=AH\cdot\left(\frac{BH}{AH}+\frac{HC}{AH}\right)\)
\(=BH+HC\)
\(=BC\) (đpcm)
c) Ta có:\(\tan B=\frac{AH}{BH}\)
Hay \(\tan\left(60\right)=\frac{6}{BH}\)
\(\Leftrightarrow BH=\frac{6}{\tan\left(60\right)}\)
\(\Leftrightarrow BH=2\sqrt{3}\)
Ta có :\(\tan\left(45\right)=\frac{AH}{HC}\)
Hay \(\tan\left(45\right)=\frac{6}{HC}\)
\(\Leftrightarrow HC=\frac{6}{\tan\left(45\right)}\)
\(\Leftrightarrow HC=6\)
Ta có :BH+HC=BC
Hay \(2\sqrt{3}+6=BC\)
\(\Leftrightarrow2\sqrt{3}+6\approx9.5\)
Ta có: SABC \(=\frac{1}{2}\cdot BC\cdot AH\)
Hay SABC\(=\frac{1}{2}6\cdot9.5\)
\(\Leftrightarrow SABC=28.5\)
Vậy SABC=28.5cm

a) \(\left(sinA+cosA\right)^2=sin^2A+cos^2A+2sinAcosA=1+2sinAcosA\)
vì tam giác \(ABC\)nhọn nên \(0^o< \widehat{A}< 90^o\)nên \(sinA>0,cosA>0\Rightarrow2sinAcosA>0\)
nên \(\left(sinA+cosA\right)^2>1\Leftrightarrow sinA+cosA>1\)do \(sinA>0,cosA>0\).
b) Kẻ đường cao \(AH\).
Đặt \(HB=x\Rightarrow HC=a-x\).
Xét tam giác \(AHB\)vuông tại \(H\): \(AH=HB.tan\widehat{ABH}=xtan45^o=x\)
Xét tam giác \(AHC\)vuông tại \(H\): \(AH=HCtan\widehat{ACH}=\left(a-x\right)tan60^o=\sqrt{3}\left(a-x\right)\)
Ta có: \(x=\sqrt{3}\left(a-x\right)\Leftrightarrow x=\frac{\sqrt{3}}{1+\sqrt{3}}a\)
\(S_{ABC}=\frac{1}{2}AH.BC=\frac{1}{2}\frac{\sqrt{3}}{1+\sqrt{3}}a.a=\frac{3-\sqrt{3}}{4}a^2\).

AC=12 BC=15
a,xét tam giác ABC có <A=90*
\(BC^2=AB^2+AC^2\)(a/dung dinh li pytago)
\(15^2=AB^2+12^2\)
\(AB^2=\sqrt{15^2-12^2}\)
AB=9
sinC=\(\dfrac{AB}{BC}\)=\(\dfrac{9}{15}\)
<C=36*
mà <B+<C=90*
->GÓC B =90-36=54

\(\left[{}\begin{matrix}\\\\\\\end{matrix}\right.\prod\limits^{ }_{ }\int_{ }^{ }dx\sinh_{ }^{ }⋮\begin{matrix}&&&\\&&&\\&&&\\&&&\\&&&\\&&&\end{matrix}\right.\Cap\begin{matrix}&&\\&&\\&&\\&&\\&&\\&&\end{matrix}\right.\)
Mình biết mỗi câu a) thôi
a) Kẻ CF vuông góc với AB
Ta có : \(\text{sinA}=\frac{CF}{AC}\); \(\text{cosA}=\frac{AF}{AC}\)
Ta có : \(sinA+cosA=\frac{AF+CF}{AC}\)
Theo bất đẳng thức tam giác trong tam giác AFC ta có \(AF+CF>AC\)
\(\Rightarrow\frac{AF+CF}{AC}>1\)(đpcm)
sin cos là sao ta?e chưa học