Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{ME}+3\overrightarrow{MC}=\overrightarrow{0}\Rightarrow\overrightarrow{MC}=-\dfrac{1}{3}\overrightarrow{ME}\)
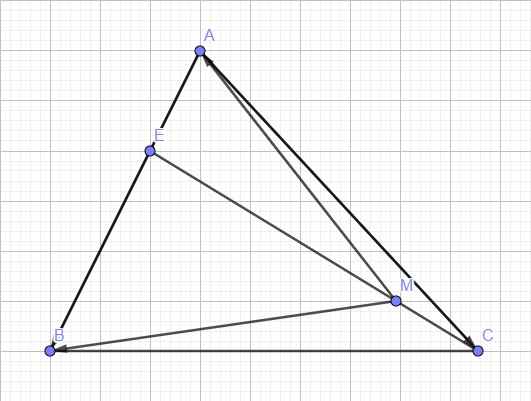
\(EB=2EA\Rightarrow\overrightarrow{BE}=2\overrightarrow{EA}\)
Ta có: \(\overrightarrow{ME}=\overrightarrow{MB}+\overrightarrow{BE}=\overrightarrow{MB}+2\overrightarrow{EA}=\overrightarrow{MB}+2\left(\overrightarrow{EM}+\overrightarrow{MA}\right)=\overrightarrow{MB}-2\overrightarrow{ME}+2\overrightarrow{MA}\)
\(\Rightarrow3\overrightarrow{ME}=\overrightarrow{MB}+2\overrightarrow{MA}\Rightarrow\overrightarrow{ME}=\dfrac{1}{3}\overrightarrow{MB}+\dfrac{2}{3}\overrightarrow{MA}\)
\(\Rightarrow\overrightarrow{MC}=-\dfrac{1}{3}\overrightarrow{ME}=-\dfrac{1}{9}\overrightarrow{MB}-\dfrac{2}{9}\overrightarrow{MA}\)
\(\Rightarrow\dfrac{2}{9}\overrightarrow{MA}=-\dfrac{1}{9}\overrightarrow{MB}-\overrightarrow{MC}\Rightarrow\overrightarrow{MA}=-\dfrac{1}{2}\overrightarrow{MB}-\dfrac{9}{2}\overrightarrow{MC}\)

Bài 2:
vecto AM=vecto AB+vecto BM
=vecto AB+2/3vecto BC
=vecto AB+2/3*(vecto BA+vecto AC)
=1/3*vecto AB+2/3*vecto AC

Tham khảo:

a) M thuộc cạnh BC nên vectơ \(\overrightarrow {MB} \) và \(\overrightarrow {MC} \) ngược hướng với nhau.
Lại có: MB = 3 MC \( \Rightarrow \overrightarrow {MB} = - 3.\overrightarrow {MC} \)
b) Ta có: \(\overrightarrow {AM} = \overrightarrow {AB} + \overrightarrow {BM} \)
Mà \(BM = \dfrac{3}{4}BC\) nên \(\overrightarrow {BM} = \dfrac{3}{4}\overrightarrow {BC} \)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\overrightarrow {BC} \)
Lại có: \(\overrightarrow {BC} = \overrightarrow {AC} - \overrightarrow {AB} \) (quy tắc hiệu)
\( \Rightarrow \overrightarrow {AM} = \overrightarrow {AB} + \dfrac{3}{4}\left( {\overrightarrow {AC} - \overrightarrow {AB} } \right) = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)
Vậy \(\overrightarrow {AM} = \dfrac{1}{4}.\overrightarrow {AB} + \dfrac{3}{4}.\overrightarrow {AC} \)