Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Xét ΔANI và ΔCNM có
AN=CN(N là trung điểm của AC)
\(\widehat{ANI}=\widehat{CNM}\)(hai góc đối đỉnh)
NI=NM(gt)
Do đó: ΔANI=ΔCNM(c-g-c)
b) Ta có: ΔANI=ΔCNM(cmt)
nên AI=MC(hai cạnh tương ứng)
Ta có: ΔANI=ΔCNM(cmt)
nên \(\widehat{IAN}=\widehat{MCN}\)(hai góc tương ứng)
mà \(\widehat{IAN}\) và \(\widehat{MCN}\) là hai góc ở vị trí so le trong
nên MC//AI(Dấu hiệu nhận biết hai đường thẳng song song)
c) Xét ΔABC có
M là trung điểm của AB(gt)
N là trung điểm của AC(gt)
Do đó: MN là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)
hay MN//BC và \(MN=\dfrac{1}{2}\cdot BC\)(Định lí 2 về đường trung bình của tam giác)
d) Xét ΔANE và ΔCNF có
NA=NC(N là trung điểm của AC)
\(\widehat{EAN}=\widehat{FCN}\)(cmt)
AE=CF(gt)
Do đó: ΔANE=ΔCNF(c-g-c)
hay \(\widehat{ANE}=\widehat{CNF}\)(hai góc tương ứng)
mà \(\widehat{ANE}+\widehat{ENC}=180^0\)(hai góc kề bù)
nên \(\widehat{CNF}+\widehat{CNE}=180^0\)
\(\Leftrightarrow\widehat{FNE}=180^0\)
hay E,N,F thẳng hàng(đpcm)

a: Xét tứ giác ABCQ có
N là trung điểm của AC
N là trung điểm của BQ
Do đó: ABCQ là hình bình hành
Suy ra: AQ//BC và AQ=BC
Xét tứ giác ACBP có
M là trung điểm của AB
M là trung điểm của CP
Do đó: ACBP là hình bình hành
Suy ra: AP//BC và AP=BC
Ta có: AQ//BC
AP//BC
mà AQ,AP có điểm chung là A
nên Q,A,P thẳng hàng
mà AP=AQ
nên A là trung điểm của PQ
b: Xét ΔABC có
M là trung điểm của AB
N là trung điểm của AC
Do đó: MN là đường trung bình
=>MN//BC và MN=BC/2
hay MN=PQ/4
=>PQ=4MN

tự kẻ hình nha
a) xét tam giác AMN và tam gáic CEN có
AN=NC(gt)
MN=NE(gt)
ANM=CNE( đối đỉnh)
=> tam giác AMN= tam giác CEN(cgc)
=> AM=CE(hai cạnh tương ứng) mà AM=MB=> MB=CE
=> CEN=AMN(hai góc tương ứng)
mà CEN so le trong với AMN mà A,M,B thẳng hàng=> MB//CE
c) từ MB//CE=> BMC=MCE( so le trong)
xét tam giác BMC và tam gíac ECM có
MC chung
BMC=MCE(cmt)
MB=CE(cmt)
=> tam gíac BMC= tam giác ECM(ccg)
d) từ tam giác BMC= tam giác CEM=> BCM=EMC( hai góc tương ứng), ME=BC( hai cạnh tương ứng)
mà BCM so le trong với EMC=> MN//BC
vì MN=NE mà ME=BC(cmt)
=> BC=2MN=> MN=1/2BC

a) Xét tam giác AMN và tam giác BMC, ta có:
MA = MB (M là trung điểm của AB)
góc NMA = góc BMC (đối đỉnh)
MN = MC (gt)
=> tam giác AMN = tam giác BMC
b) Xét tứ giác ACBN, ta có:
M là trung điểm của AB (gt)
M là trung điểm của CN (MC = MN)
=> Tứ giác ACBN là hình bình hành
=> AN // BC
c) Do tứ giác ACBN là hình bình hành => AN // BC và AN = BC => góc ANC = góc BCN và AN = BC
Xét tam giác NAC và tam giác CBN, ta có:
AN = BC (cmt)
góc ANC = góc BCN (cmt)
CN chung
=> tam giác NAC = tam giác CBN

a) Sửa đề: ΔAMB=ΔDMC
Xét ΔAMB và ΔDMC có
MA=MD(gt)
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC(M là trung điểm của BC)
Do đó: ΔAMB=ΔDMC(c-g-c)

a) Xét tam giác ABN và tam giác ACM có:
\(\widehat{A}\):góc chung
AM=AN(gt)
AC=AB(tam giác ABC cân)
Suy ra \(\Delta ABN=\Delta ACM\)(c.g.c)
b)Xét tam giác AMN. Do AM=AN(gt) nên tam giác này là tam giác cân
Suy ra \(\widehat{M}=\widehat{N}=\frac{180^o-\widehat{A}}{2}\)(1)
Lại xét tam giác ABC cân nên:
\(\widehat{B}=\widehat{C}=\frac{180^o-\widehat{A}}{2}\)(2)
Từ (1) và (2), suy ra:
\(\widehat{M}=\widehat{B}\) và \(\widehat{N}=\widehat{C}\)
Mà các cặp góc này đều có các góc ở vị trí so le trong nên MN//BC(đpcm)

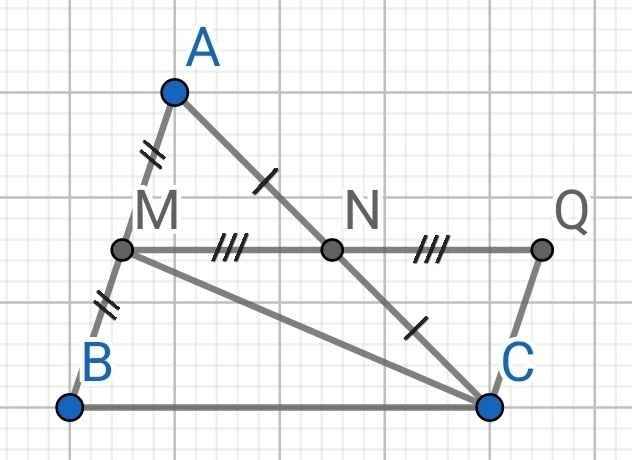
a) Xét ∆AMN và ∆CQN có:
AN = NC (do N là trung điểm của AC)
∠ANM = ∠CNQ (đối đỉnh)
NM = NQ (gt)
⇒ ∆AMN = ∆CQN (c-g-c)
b) Do ∆AMN = ∆CQN (cmt)
⇒ ∠MAN = ∠NCQ (hai góc tương ứng)
Mà ∠MAN và ∠NCQ là hai góc so le trong
⇒ AM // CQ
⇒ MB // CQ
c) Do ∆AMN = ∆CQN (cmt)
⇒ AM = CQ (hai cạnh tương ứng)
Mà AM = MB (do M là trung điểm của AB)
⇒ MB = CQ
Do BM // CQ (cmt)
⇒ ∠BMC = ∠QCM (so le trong)
Xét ∆BMC và ∆QCM có:
BM = CQ (cmt)
∠BMC = ∠QCM (cmt)
CM là cạnh chung
⇒ ∆BMC = ∆QCM (c-g-c)
⇒ BC = MQ (hai cạnh tương ứng)
Do NM = NQ (gt)
⇒ MN = 1/2 MQ
Mà BC = MQ (cmt)
⇒ MN = 1/2 BC