Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Có \(\overrightarrow{AN}=\overrightarrow{AB}+\overrightarrow{BN}\)
\(\overrightarrow{BP}=\overrightarrow{BC}+\overrightarrow{CP}\)
\(\overrightarrow{CM}=\overrightarrow{CA}+\overrightarrow{AM}\)
Cộng vế vs vế:
\(\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{BN}+\overrightarrow{CP}+\overrightarrow{AM}\)
\(=\overrightarrow{AC}+\overrightarrow{CA}+\frac{1}{3}\left(\overrightarrow{BC}+\overrightarrow{CA}+\overrightarrow{AB}\right)\)
\(=0+\frac{1}{3}\left(\overrightarrow{BA}+\overrightarrow{AB}\right)=0\) (đpcm)

Lời giải:
\(\overrightarrow{MN}=\overrightarrow{MB}+\overrightarrow{BN}=\overrightarrow{MB}+\overrightarrow{BC}+\overrightarrow{CN}\)
\(=\overrightarrow{MB}+\overrightarrow{BC}+2\overrightarrow{BC}=\overrightarrow{MB}+3\overrightarrow{BC}\)
\(=\overrightarrow{MA}+\overrightarrow{AB}+3(\overrightarrow{BA}+\overrightarrow{AC})\)
\(=-\overrightarrow{AM}+\overrightarrow{AB}-3\overrightarrow{AB}+3\overrightarrow{AC}\)
\(=-\frac{1}{3}\overrightarrow{AB}+\overrightarrow {AB}-3\overrightarrow{AB}+3\overrightarrow{AC}\)
\(=\frac{-7}{3}\overrightarrow{AB}+3\overrightarrow{AC}\)
Ta có đpcm.

\(\overrightarrow{AN}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}=\frac{\overrightarrow{AB}}{2}+\frac{\overrightarrow{AC}}{2}=\overrightarrow{AM}+\overrightarrow{AP}\)
\(\overrightarrow{AN}=\frac{\overrightarrow{AB}+\overrightarrow{AC}}{2}\)
\(\overrightarrow{BP}=\frac{\overrightarrow{BA}+\overrightarrow{BC}}{2}\)
\(\overrightarrow{CM}=\frac{\overrightarrow{CB}+\overrightarrow{CA}}{2}\)
\(\Rightarrow\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\frac{\overrightarrow{AB}+\overrightarrow{AC}+\overrightarrow{BA}+\overrightarrow{CA}+\overrightarrow{BC}+\overrightarrow{CB}}{2}=\overrightarrow{0}\)

a/ \(\overrightarrow{AN}+\overrightarrow{BP}+\overrightarrow{CM}=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{AC}\right)+\frac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{BA}\right)+\frac{1}{2}\left(\overrightarrow{CA}+\overrightarrow{CB}\right)\)
\(=\frac{1}{2}\left(\overrightarrow{AB}+\overrightarrow{BA}\right)+\frac{1}{2}\left(\overrightarrow{AC}+\overrightarrow{CA}\right)+\frac{1}{2}\left(\overrightarrow{BC}+\overrightarrow{CB}\right)=\overrightarrow{0}\)
b/
Do MN là đường trung bình tam giác ABC \(\Rightarrow\overrightarrow{MN}=\frac{1}{2}\overrightarrow{AC}\)
\(\overrightarrow{AN}=\overrightarrow{AM}+\overrightarrow{MN}=\overrightarrow{AM}+\frac{1}{2}\overrightarrow{AC}=\overrightarrow{AM}+\overrightarrow{AP}\)
c/
\(\overrightarrow{AM}+\overrightarrow{BN}+\overrightarrow{CP}=\frac{1}{2}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{BC}+\frac{1}{2}\overrightarrow{CA}=\frac{1}{2}\overrightarrow{AC}+\frac{1}{2}\overrightarrow{CA}=\overrightarrow{0}\)

\(\overrightarrow{AM}=\overrightarrow{AB}+\overrightarrow{BM}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{BC}\)
\(=\overrightarrow{AB}+\dfrac{2}{3}\left(\overrightarrow{BA}+\overrightarrow{AC}\right)\)
\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{2}{3}\overrightarrow{AC}\)
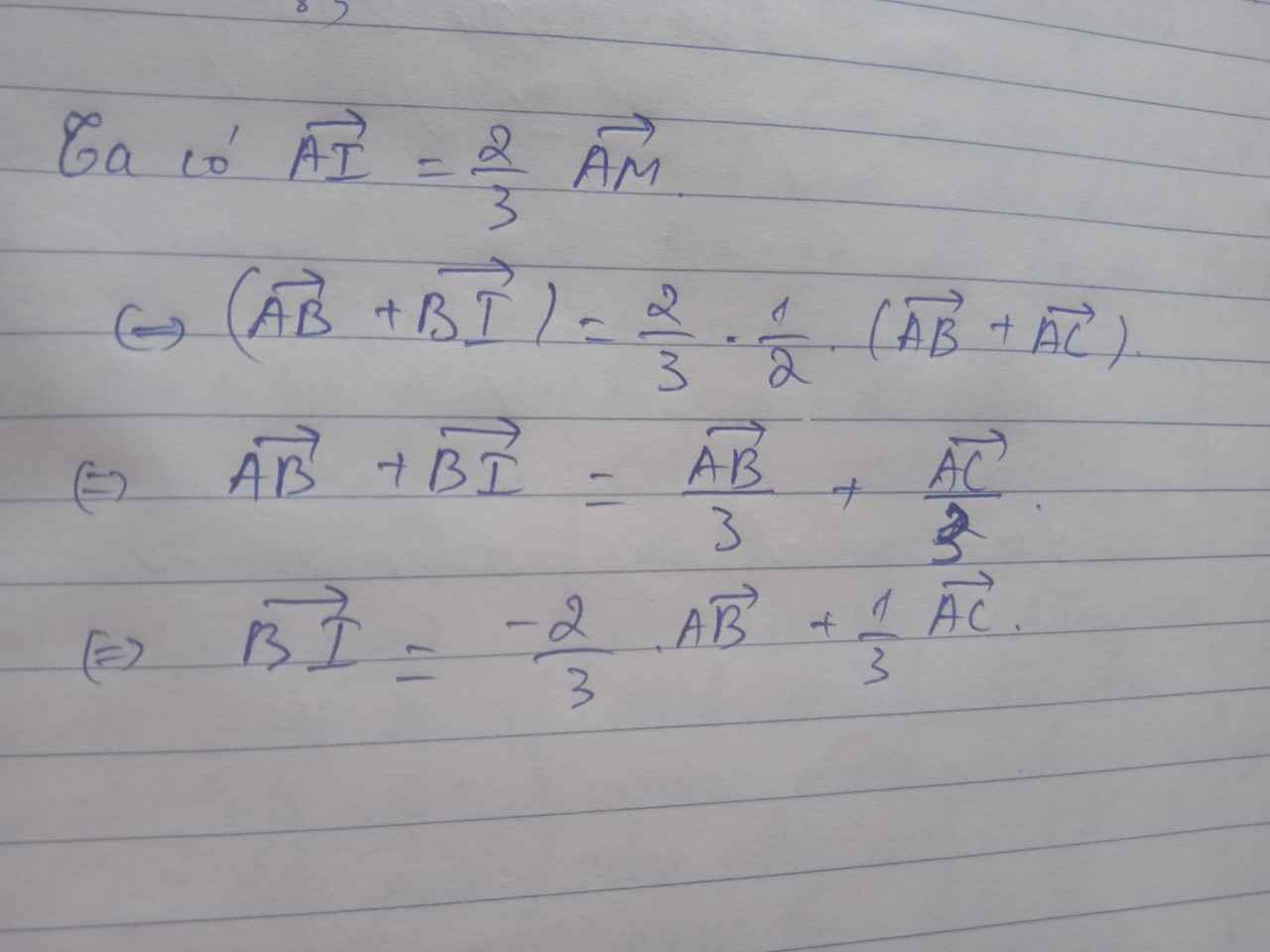


Ta có :
\(\overrightarrow{BP}+\overrightarrow{AN}+\overrightarrow{CM}=\overrightarrow{BC}+\overrightarrow{CP}+\overrightarrow{AB}+\overrightarrow{BN}+\overrightarrow{CA}+\overrightarrow{AM}=\overrightarrow{CP}+\overrightarrow{BN}+\overrightarrow{AM}\)\(=\dfrac{1}{3}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{BC}+\dfrac{1}{3}\overrightarrow{CA}\)
\(=\dfrac{1}{3}\left(\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CA}\right)\)
\(=\dfrac{1}{3}\overrightarrow{0}\)
\(=\overrightarrow{0}\)
\(\RightarrowĐPCM\)