Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC=BD
c: ABDC là hình bình hành
=>AB//DC

a. Xét △ABM và △DCM:
\(AM=MD\left(gt\right)\)
\(\hat{AMB}=\hat{DMC}\) (đối đỉnh)
\(BM=MC\left(gt\right)\)
\(\Rightarrow\Delta ABM=\Delta DCM\left(c.g.c\right)\)
b. Từ a. => \(\hat{MCD}=\hat{MBA}\) (2 góc tương ứng). Mà hai góc này ở vị trí so le trong
\(\Rightarrow CD\text{ // }AB\left(a\right)\)
c. Xét △CIK và △AIB:
\(AI=IC\left(gt\right)\)
\(\hat{AIB}=\hat{CIK}\) (đối đỉnh)
\(BI=IK\left(gt\right)\)
\(\Rightarrow\Delta CIK=\Delta AIB\left(c.g.c\right)\Rightarrow\hat{ICK}=\hat{IAB}\). Mà hai góc ở vị trí so le trong
\(\Rightarrow AB\text{ // }CK\left(b\right)\)
Từ (a) và (b), theo tiên đề Ơ-clit \(\Rightarrow AB\text{ // }DK\)
Vậy: D, C, K thẳng hàng (đpcm).
a) Xét tam giác ABM và tam giác DCM:
BM = CM (M là trung điểm BC).
\(\widehat{AMB}=\widehat{DMC}\) (đối đỉnh).
MA = MD (cmt).
\(\Rightarrow\) Tam giác ABM = Tam giác DCM (c - g - c).
b) Ta có: \(\widehat{BAM}=\widehat{CDM}\) (Tam giác ABM = Tam giác DCM).
Mà 2 góc này ở vị trí so le trong.
\(\Rightarrow\) CD // AB (dhnb).
c) Xét tứ giác AKCB có:
I là trung điểm AC (gt).
I là trung điểm BK (IB = IK).
\(\Rightarrow\) Tứ giác AKCB là hình bình hành (dhnb).
\(\Rightarrow\) CK // AB (Tính chất hình bình hành).
Mà CD // AB (cmt).
\(\Rightarrow\) D, C, K thẳng hàng.

a. Để chứng minh tam giác ABM bằng tam giác DCM, ta có:
Vì M là trung điểm của BC, nên BM = MC.Vì MD = MA, nên tam giác AMD là tam giác cân tại A.Từ đó, ta có AM = AD.Vì BM = MC và AM = AD, nên tam giác ABM và tam giác DCM có cạnh bằng nhau và góc tương ứng bằng nhau.Do đó, tam giác ABM bằng tam giác DCM.b. Để chứng minh AC song song và bằng BD, ta có:
Vì B là trung điểm của AC, nên AB = BC.Vì MD = MA, nên tam giác AMD là tam giác cân tại A.Từ đó, ta có AM = AD.Vì AB = BC và AM = AD, nên tam giác ABM và tam giác DCM có cạnh bằng nhau và góc tương ứng bằng nhau.Do đó, AC song song và bằng BD.c. Để chứng minh B, M, Q thẳng hàng và M trung trực AK, ta có:
Vì B là trung điểm của AC và Q là trung điểm của BC, nên BQ song song với AC và BQ = 1/2 AC.Vì M là trung điểm của BC, nên MQ song song với AC và MQ = 1/2 AC.Vì BQ song song với AC và MQ song song với AC, nên B, M, Q thẳng hàng.Vì M là trung điểm của BC, nên AM là đường trung trực của BC.Vậy, ta đã chứng minh được các phần a, b, c.
a: Xét ΔABM và ΔDCM có
MA=MD
góc AMB=góc DMC
MB=MC
=>ΔABM=ΔDCM
b: Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
=>AC//BD và AC=BD

a: Xét ΔABM và ΔACM có
AB=AC
AM chung
BM=CM
DO đó: ΔABM=ΔACM
b: Xét ΔABM và ΔDCM có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)
MB=MC
Do đó: ΔABM=ΔDCM
Xét tứ giác ABDC có
M là trung điểm của BC
M là trung điểm của AD
Do đó: ABDC là hình bình hành
Suy ra: AB//DC

a: Xét ΔMAB và ΔMDC có
MA=MD
\(\widehat{AMB}=\widehat{DMC}\)(hai góc đối đỉnh)
MB=MC
Do đó: ΔMAB=ΔMDC
b: Ta có: ΔMAB=ΔMDC
=>\(\widehat{MAB}=\widehat{MDC}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AB//CD
Ta có: AB//CD
AB\(\perp\)AC
Do đó: CD\(\perp\)CA
Xét ΔABC vuông tại A và ΔCDA vuông tại C có
AB=CD
AC chung
Do đó: ΔABC=ΔCDA
c: Ta có: ΔABC=ΔCDA
=>BC=DA
Xét ΔMCA và ΔMBD có
MC=MB
\(\widehat{CMA}=\widehat{BMD}\)(hai góc đối đỉnh)
MA=MD
Do đó: ΔMCA=ΔMBD
=>\(\widehat{MCA}=\widehat{MBD}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Ta có: AC//BD
AC\(\perp\)CD
Do đó: DC\(\perp\)DB
=>ΔDBC vuông tại D
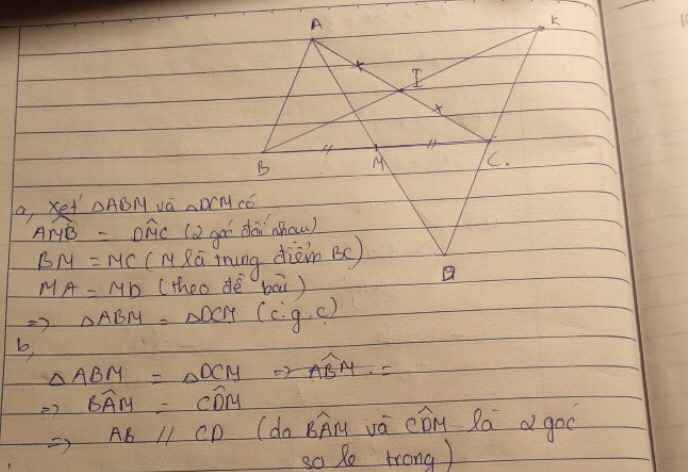
a) Xét \(\Delta ABMvà\Delta DCMcó:\)
MB=MC
góc AMB=góc CMD
MA=MD
\(\Rightarrow\Delta ABM=\Delta DCM\left(c-g-c\right)\)
b) Xét \(\Delta AMCvà\Delta BMDcó:\)
MC=MB
góc AMC=góc BMD
MA=MD
\(\Rightarrow\Delta AMC=\Delta DMB\left(c-g-c\right)\)
\(\Rightarrow AC=BD\)(cặp cạnh tương ứng)
c) Theo a), \(\Delta ABM=\Delta DCM\Rightarrow\)góc ABM=góc DCM (cặp góc tương ứng)
Mà 2 này tạo với BC hai góc so le trong nên AB//CD