Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
cho tam giác ABC có AD là tia phân giác.Biết AB= c , AC= b , Tính độ dài cạnh AD theo b , c và góc A


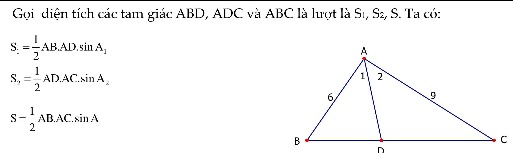
SABC=SADB+SADCSABC=SADB+SADC
<=>bc.sinA=AD⋅c⋅sinA2+AD⋅b⋅sinA2bc.sinA=AD⋅c⋅sinA2+AD⋅b⋅sinA2
<=>bc.sinA=AD⋅sinA2(b+c)bc.sinA=AD⋅sinA2(b+c)
<=>bc.sin2α=AD⋅sinα(b+c)bc.sin2α=AD⋅sinα(b+c)
<=>2bc.sinα.cosα=AD⋅sinα(b+c)2bc.sinα.cosα=AD⋅sinα(b+c)
<=>AD=2bc⋅cosαb+cAD=2bc⋅cosαb+c (dpcm)
a) Xét tam giác HAB và tam giác ABC có:
Góc AHB= góc BAC (= 900 )
B> là góc chung
⇒ tam giác HAB ~ tam giác ABC (g.g)
b) Xét ΔΔ ABC vuông tại A: BC2 = AB2 + AC2
Hay BC2 = 122 + 162
BC2 = 144 + 256 = 400
=> BC = √400 = 20 (cm)
Ta có : Δ HAB ∼ Δ ABC
=> HAAB=ABBCHAAB=ABBC
Hay HA12=1220HA12=1220
=> AH = 12.1220=7,212.1220=7,2 cm
c)
Ta có
DE là tia phân giác của góc ADB trong tam giác DAB,
áp dụng t/c tia phân giác thìDADB=AEEBDADB=AEEB
DG là tia phân giác cảu góc CDA trong tam giác CDA.
áp dụng t/c tia phân giác thì CDDA=CFFACDDA=CFFA
VẬy EAEB.DBDC.FCFA=DADB.DBDC.CDDA=1EAEB.DBDC.FCFA=DADB.DBDC.CDDA=1(dpcm)

a: Xét ΔABC có góc A+góc B+góc C=180 độ
=>góc A=180 độ-30 độ-20 độ=130 độ
Xét ΔABC có BC/sinA=AC/sinB=AB/sinC
=>AC/sin30=AB/sin20=30/sin130
=>\(AC\simeq19,58\left(cm\right);AB\simeq13,39\left(cm\right)\)
ΔAHB vuông tại H có sin B=AH/AB
=>AH/13,39=1/2
=>AH=6,695(cm)
b: Xét ΔABC có AD là phân giác
nên AB/AC=BD/DC
=>\(\dfrac{BD}{DC}=\dfrac{13.39}{19.58}\)
=>\(\dfrac{BD}{13.39}=\dfrac{CD}{19.58}\)
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{13.39}=\dfrac{CD}{19.58}=\dfrac{BD+CD}{13.39+19.58}=\dfrac{30}{32.97}=\dfrac{1000}{1099}\)
=>\(BD\simeq12,18\left(cm\right);CD\simeq17,82\left(cm\right)\)

b) xét ∆ABC có AD là đường phân giác của góc A
=>BD/AB=DC/AC ( tính chất)
Áp dụng tính chất dãy tỉ số bằng nhau , được :
BD/AB=DC/AC=BD/6=DC/8=(BD+DC)/(6+8)=BD/14=10/14=5/7
==>BD=6×5:7≈4,3
==>DC=10-4,3≈5,7
a,Áp dụng định lý Pi-ta-go vào tam giác ABC => tam giác ABC vuông tại A=> AH vuông góc vs BC
=> tam giác ABC đồng dạng vs tam giác HAC ( g.c.g)
b, Vì tam giác ABC vuông tại A nên ta có hệ thức: AC2=BC . HC => đpcm
c, có AD là tia phân giác của tam giác ABC => BD=CD=BC/2= 5cm
Mình nghĩ đề bạn thiếu đó.
đề đủ đó bạn